Másodfokú egyenlet (megoldások)
Az igény, hogy az egyenlet megoldásához nem csak az első, hanem a második fokozatot az ókorban okozta, hogy a problémák megoldására járó megtalálni a földterület és földmunka egy katonai jellegű, valamint a fejlesztési csillagászat és a matematika is.
Az egyenlet a formájában ax 2 + bx + c = 0, ahol a. b. c - valós számok, ahol a ≠ 0, az úgynevezett egy másodfokú egyenlet.
Ha a = 1 hívják másodfokú egyenlet adni; Ha egy ≠ 1, a nem redukált.
A. b. c az alábbi címek: a - egy első tényező, b - a második tényező, c - konstans.
A gyökerek a egyenlete ax 2 + bx + c = 0 található, amelyet a képlet
Az expressziós D = b 2 - 4ac úgynevezett diszkriminánsa másodfokú egyenlet.
- ha D <0, то уравнение не имеет действительных корней;
- Ha D = 0, az egyenlet van egy valódi gyökér;
- ha D> 0, az egyenlet két valós gyöke.
Abban az esetben, ha D = 0, néha azt mondják, hogy a másodfokú egyenlet két azonos gyökér.
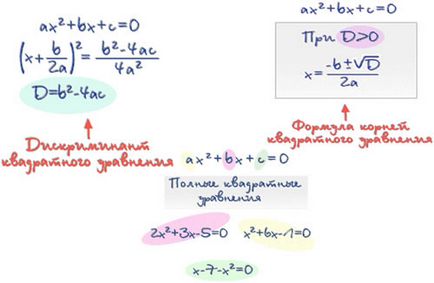
Teljes másodfokú egyenlet
Hiányos másodfokú egyenletek
Ha a másodfokú egyenlet ax 2 + bx + c = 0 második együtthatójának b, és a konstans c egyenlő nulla, egy másodfokú egyenlet nevezzük hiányos.
Hiányos egyenlet visszaállítani, mivel annak érdekében, hogy megtalálják a gyökerekhez, nem tudja használni a képlet a másodfokú egyenlet gyökerek - könnyebb megoldani az egyenletet a bomlás a bal oldalára történő tényezők.
Megoldási módjait, a másodfokú egyenletek hiányos:
Határozat hiányos másodfokú egyenlet
Másodfokú egyenlet komplex változók
Először azt a legegyszerűbb másodfokú egyenlet 2 z = a. ahol egy-előre meghatározott számú, és a Z-ismeretlen. A valós számok halmaza, ez az egyenlet:
- van egy gyökere z = 0, ha a = 0;
- Két igazi z1, gyökér 2 = ± √a
- Nincs valódi gyökereit, ha a <0
A megoldás a másodfokú egyenlet grafikonok
Anélkül képlet segítségével másodfokú egyenlet megoldásából grafikusan. Például x 2 + x + 1 = 0.
Mi megoldjuk az egyenletet. Erre a célra konstrukció két grafikon y = x 2; y = x + 1.
y = x 2 másodfokú függvény grafikon parabola.
y = x + 1, a lineáris függvény vonal grafikon.
A grafikonok metszik két pontot, az egyenletnek két gyöke.
Válasz: x ≈ -0,6; x ≈ 2,6.
A problémák megoldását használva másodfokú egyenlet