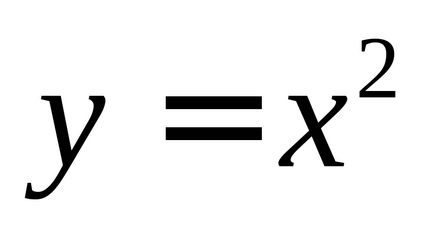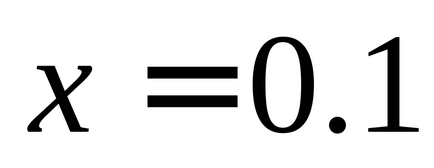Lab 7-1 metsző és érintőleges
Laboratóriumi munka № 7-1
A geometriai jelentése SZÁRMAZÉKOS
A származék egy folytonos függvény egyik legfontosabb jellemzőit. Ezt alkalmazzák a probléma kivizsgálása viselkedését a funkciót, építését a menetrend, a szűkített és korlátozásoktól optimalizálása, és még sokan mások. A származék egy folytonos függvény egy változó egy adott pontban x definiált, mint a határérték, a viszonyítva az növekmény a növekmény az utolsó argumentum nullához:
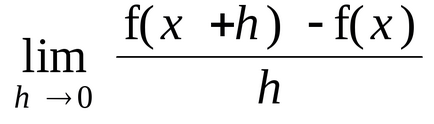
Kiszámításához származék speciális parancs diff () létezik Maple, amely lehetővé teszi, hogy kiszámítja a származékok bármilyen sorrendben egyváltozós függvényeket és a parciális deriváltjai funkciói több változó.
Geometriai értelmében a származék. Az érintő a függvény grafikonját
Kezdjük bemutató részben a geometriai jelentése a-származék, mint a lejtőn a érintő a grafikon az adott pont. A tangens úgy definiáljuk, mint a korlátozó helyzetében a szekáns áthaladó két pont a grafikon hajlamos az egyik a másik. Minden az építkezések zajlanak a példa a funkció:
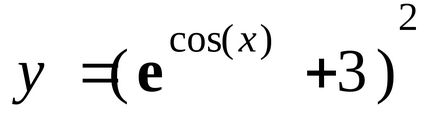
Kiszámítjuk a származék a ponton x0 = 1. Ehhez, definiáljuk a funkciót is, és annak két pontot a grafikon a abszcisszára, x0 = 1, és x1 = x0 + H:
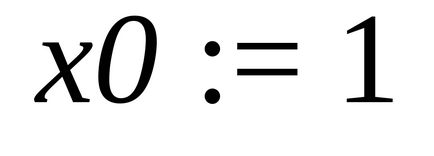
meredeksége () parancsot (meredekség) a hallgató csomag kiszámítja az érintő hajlásszöge áthaladó két megadott pont:
> A (hallgató): t: = meredekség (P0, P1);
Most, ha hagyjuk, hogy h, hogy nulla, akkor az expressziós t kell konvergálnak számos egyenlő a lejtőn a szekáns a véghelyzet, azaz a lejtőn a érintő a függvény grafikonját az x = 1. Mi határozza meg a szekvencia h_values értékek nullához:
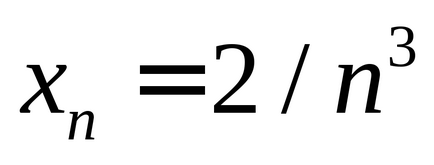
> Seq (evalf (t), h = h_values);
-5,439033250, -12,57034624, -13,3498521, -13,5137879, -13,569058,
-13.592932, -13,604946, -13,611648, -13,615686, -13,61826,
Nyilvánvaló, hogy ez a sorozat konvergál, és nagyon gyorsan. De ha konvergál az érték a függvény deriváltját x = 1? Kiszámítjuk a származék keresztül diff () függvényt:
eval parancs helyett számszerű értékeket egy funkciót. evalf csapat - kiszámítani a hozzávetőleges értéke a kifejezés.
Megjegyezzük, hogy az általunk épített a szekvenciát konvergál értéke a származék x pontban = 1. Már a tizenötödik elemnek két pontos tizedes. Pontos eredményt kapunk, ha kiszámítjuk a határát az expressziós t h 0:
Maple grafikus képességek lehetővé teszik, hogy milyen a szelő közelít az érintő. Construct egyenlet egy szelő áthaladó két adott pont a koordináták (x0, y (x0)) és (X0 + H, Y (X0 + H)), illetve (ahol Y jelentése a függő és független változók X):
Mi kifejezni a függő változó Y egy független X és képviselt függvényében:
unapply parancs alakítja a kifejezés arra a funkcióra. A csapat jobb oldala azt jelenti: „jobb oldali” - a jobb oldalon a kifejezés. % Azt jelenti, az eredmény az előző műveletet. Megvan az egyenlet a vágás.
Hasonlóképpen, megkonstruálunk függvényében egyenlete az érintő. Ez használ ismert egyenlettel az érintő.
Most tudjuk építeni képek sorozata tartalmazó függvény grafikonját, annak érintője és metsző, amikor a H paramétert, és megjeleníti azt a formájában animált képmegjelenítés () parancsot:
> S: = azt követő (plot ([y (x), line_tang (x), line_sec (x)], x = 0..4,
nézet = [0..3,10..40], színes = [fekete, fekete, zöld], vastagsága = 2)
> A (parcellák): kijelző (S, insequence = true);
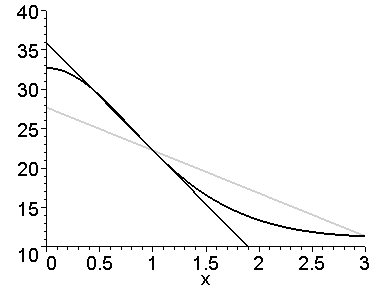
TASK 1. Oldjuk meg a hasonló problémákkal kérve más szekvenciákat h_values Cut lassabb lesz keresni egy érintő ha
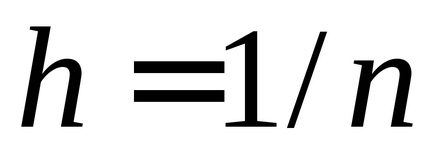
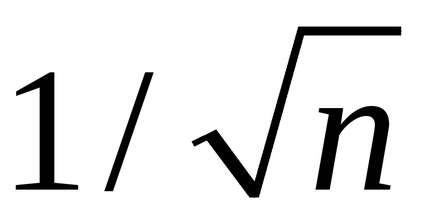
TASK 2. Fedezze közelítéséről szelő a tangens függvény