Inverz trigonometrikus függvények, tulajdonságaik és grafikonok
Inverz trigonometrikus függvények (Arkuszszinusz, Arkuszkoszinusz, cotanges és inverz kotangensét) a fő elemi függvények. Gyakran miatt előtag „bárka” inverz trigonometrikus függvények úgynevezett arkfunktsiyami. Most nézzük a menetrendek és a lista tulajdonságait.
Arkusz szinusz függvény y = arcsin (x).
Képzeljük grafikon az inverz szinusz függvény:
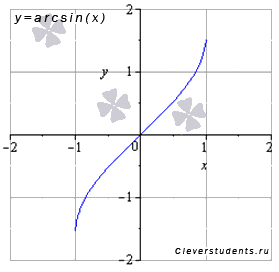
Tulajdonságok arkusz szinusz függvény az y = arcsin (x).
· A tartomány az ív szinusz függvény az intervallum otminus egység és magában :.
· Az értékek függvényében y = arcsin (x). .
· Arkuszszinusz funkció - páratlan ettől.
· A funkció y = arcsin (x) növeli az egész tartományban, azaz ha.
· Homorú funkciót. domború.
· Inflexiós pontja (0; 0). ez egy nulla funkciót.
Vissza az elejére
Arkusz függvény y = arccos (x).
Ábrázolja az inverz koszinusz függvény formájában:
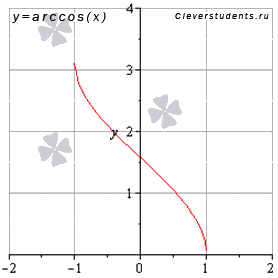
Tulajdonságok arkusz függvény az y = arccos (x).
· A domain a funkció Arkuszkoszinusz :.
· Az értékek függvényében y = arccos (x). .
· A funkció nem még nem furcsa, hogy van, ez egy gyakori látvány.
· Arkuszkoszinusz működése csökken az egész tartomány, azaz mikor.
· Homorú funkciót. domború.
Vissza az elejére
Cotanges függvény y = arctg (x).
Ütemezése arkusz tangens függvény formájában:
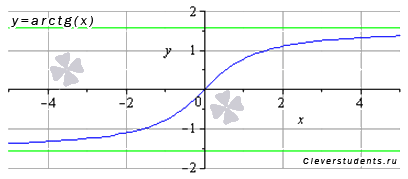
Tulajdonságok cotanges függvény az y = arctg (x).
· A domain a funkció y = arctg (x). .
· Az értékek az arkusz tangens funkciókat.
· Cotanges funkció - páratlan ettől.
· A funkció növeli a saját domain, azaz akkor, amikor.
· A funkció arc tg homorú meg. domború.
· Inflexiós pontja (0; 0). ez egy nulla funkciót.
· Horizontális asymptote közvetlen mikor és. A rajzon vannak zöld színnel.
Vissza az elejére
Inverz kotangensét függvény az y = arcctg (x).
Képzeljük grafikon az inverz kotangensét funkció:
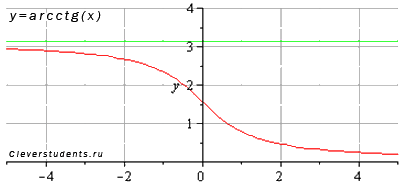
Tulajdonságok inverz kotangensét függvény az y = arcctg (x).
· A domain a funkció inverze kotangensét a teljes valós számok halmaza.
· Az értékek függvényében y = arcctg (x). .
· Inverz kotangensét funkció sem egyenletes, sem furcsa, hogy van, ez egy gyakori látvány.
· A funkció csökken a teljes domain, azaz akkor, amikor.
· Homorú funkciót. domború.
· Vízszintes aszimptotákkal egyenesek, amikor (az ábrán bemutatott zöld) és y = 0 meg.