Faktor-kritikus gráf
Kritikus tényező gráf maximális megfelelő részgráfok eltávolításával kapott az egyik csúcsot.
Kritikus faktor gráf (vagy közel sochetaemy grafikon.) - egy grafikon, n csúcsú, ahol minden egyes al-dobozok n - 1 van egy tökéletes illesztés csúcsok. (A tökéletes párosítás, a grafikon - egy részhalmaza az élek a tulajdonság, hogy az egyes csúcsok egy végső csúcs pontosan egy él a részhalmaza.)
A kombináció, amely magában foglalja az összes csúcsot, kivéve egyet, azt mondta, hogy szinte tökéletes illeszkedés. Így az azonos faktor-kritikus gráf - egy grafikon, amely már közel teljes párosítás, amely nem tartalmaz sem a csúcsot.
Három szám barátságok. Példák a nem-Hamilton faktor-kritikus gráfok
Bármilyen furcsa ciklus hossza a kritikus tényező. valamint bármely teljes gráf páratlan számú csúccsal. Általánosabban bármilyen Hamilton gráf páratlan csúcsok száma a kritikus tényező. Grófok barátságok (oszlopok összekapcsolódásával képződött egy sor háromszögek egy közös vertex) példákat a grafikonok, a kritikus tényező, de nem Hamilton.
Ha G egy kritikus tényező, ez mychelskianom gráf Például, a grafikon Grocha. mychelskian ciklus öt csúcsot, ez a kritikus tényező.
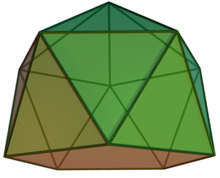
Bármilyen vertex 2-csatlakoztatott körmös-mentes gráf páratlan számú csúcsok kritikus tényező. Például egy gráfot csúcsot 11 kialakított csúcsok egy ikozaéder (grafikon sodrott hosszúkás ötszögletű piramisok [en]), olyan, mint egy 2-csatlakoztatva, és mentes a karom, úgy, hogy ez egy kritikus tényező. Ez az eredmény közvetlenül következik a alaptétele, hogy minden csatlakoztatott karom nélküli gráf páros számú pontú teljes párosítás.
Kritikus tényező diagramok leírható számos különböző módon, eltérő meghatározása a grafikonok, eltávolítjuk a vertex, amely lehetővé teszi, hogy tökéletes illeszkedés:
- Gallai Tibor [en] bebizonyította, hogy a gráf egy tényező kritikus akkor, ha az csatlakoztatva van, és minden v csúcs, van egy maximális egyezés. amely nem tartalmazza v. Ebből az is következik, hogy a grafikon páratlan csúcsok száma, és hogy minden a maximális egyezés tartalmaznia kell minden, de az egyik csúcsot.
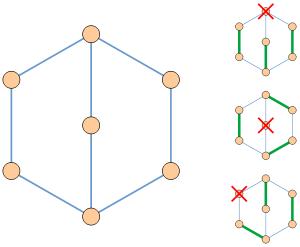
- László Lovas bebizonyította, hogy a gráf egy tényező kritikus akkor és csak akkor, ha van egy furcsa füle bomlás. partíció bordák sorozata részgráfok amelyek mindegyike az útvonal vagy a ciklus páratlan hosszúságú, és az első al-dobozok a szekvencia egy ciklus minden utat a sorozat véges, de nem a belső csúcsok előző részgráfok, és minden ciklus különbözik az első, pontosan egyik csúcsa közös a korábbi részgráfok. Például a grafikon az ábrán is tört ily módon öt ciklus élek és módon három élek. Abban az esetben, ha szinte tökéletesen megfelelő kritikus tényező grafikon is adott, fülészeti bomlás lehet választani úgy, hogy minden fül kiterjed felváltva illő élek és szélek nem szerepel a megfelelő.
- Graf szintén tényező kritikus akkor és csak akkor lehet csökkenteni a grafikon egyetlen csúcs meghúzásával ciklus páratlan hosszúságú. Sőt, ebben az esetben lehetőség van arra, hogy válasszon minden ciklusban szekvenciáját, hogy az tartalmazza a vertex összehúzódása az előző ciklusban. Például, ha a pull fül fül bomlás által meghatározott sorrendben bomlik, minden alkalommal összehúzódásra fül alkot egy furcsa ciklus, hogy a leírás segítségével egy fül bomlás lehet használni, hogy keressen a sorozat páratlan ciklus összehúzódás. Ezzel szemben, a szekvenciáját összehúzódások páratlan ciklusokban tartalmazó kapott csúcs az előző összehúzódások képezhető a fülben bővítése, ahol több fül képződik összehúzható élek.
- Tegyük fel, hogy a G gráf adják a kijelölt csúcsok v és egy megfelelő M. amely kiterjed az összes csúcsok kivételével v. Akkor G-faktor-kritikus, ha és csak akkor, ha számos módja van a G. álló felváltva elérte a széleit a párosítások és a bordák, nem egyező, amely összeköti a v csúcs az összes többi csúcsainak G. alapján az ingatlan, megadhatjuk, lineáris időben. G A grafikon és a készlet szinte tökéletes illesztés faktor-kritikus.
Faktor-kritikus gráfok mindig páratlan számú csúcsa, és meg kell szélű 2-kapcsolt (azaz, hogy nem lehet semmilyen híd). Ezek azonban nem feltétlenül Vertex 2-csatlakoztatva. Számít barátságok olyan ellenpélda. Faktor-kritikus gráf nem lehet páros. a páros gráf szinte tökéletes egyezés csak a csúcsok, hogy lehet eltávolítani, így a tökéletes illesztés a grafikon, vannak a nagyobb oldalon a páros gráf.
Bármilyen vertex 2-egy csatlakoztatott hányadosa kritikus gráf m bordák már legalább M számú különböző majdnem tökéletes párosítások, és még általánosabban, bármely faktor-kritikus gráfot m élek, és C egységek (összefüggő komponense 2 csúcs) van legalább m - c + 1 különböző szinte teljes párosítás. Grafikon, amelyekre ezek a határok pontos, lehet leírni, mint amelyek a fül bomlása bizonyos fajok.
Bármely csatlakoztatott gráf átalakítható faktor-kritikus gráf meghúzásával egy csomó bordák. A minimális élek halmaza, hogy meg kell húzni együtt, hogy egy adott G gráf egy kritikus tényező, az alapja egy matroid. Tény, ami azt mutatja, hogy a dolgozó polinomiális mohó algoritmus lehet használni, hogy keressen a legalacsonyabb súlyozott sor bordák, összehúzódást ami a számlálás kritikus tényező. Korai összehúzódás algoritmus minimális száma (súlyozatlan) élek, hogy elérjék a kritikus tényező grafikon megtalálható egy cikket Frank.
Virág - tényező kritikus részgráf és a grafikon. Virág kulcsszerepet játszanak az algoritmusok [en] Edmonds [en] Keresés maximális és minimális megfelelő súlyozott tökéletes kombináció nem páros gráf.
A kombinatorika Poliéderek faktor-kritikus gráfok fontos szerepet játszanak a leíró szempontjára poliéder párosítást egy adott gráf.
Az általánosítások és a kapcsolódó fogalmak szerkesztése
Azt mondják, hogy a gráf k-tényező kritikus, ha bármely részhalmaza n - k pontú teljes párosítás. Ezzel a meghatározással, szinte kompatibilis (hu: hypomatchable) gráf egy 1-faktor-kritikus. Még általánosabban, egy grafikon (a, b) a-faktor-kritikus, ha bármely alcsoportja az n - k csúcs r-faktor, azaz egy sor r-reguláris csúcsai a részgráf adott gráf.
Amikor az emberek beszélnek a kritikus oszlopon (megadása nélkül k-), általában utalva a grafikon, eltávolítását bármely csúcspont, amely csökkenti a színek számát szükséges gráfszınezés. A koncepció a kritikusság használják sokkal szélesebb körben gráfelmélet grafikonok, amelyben az eltávolítását bármely csúcspont változtatni tulajdonság a gráf. Kritikus kombinációi grafikon - egy grafikon, amely az eltávolítása bármelyik csomópont nem változik a méret a maximális egyezés. Szerint Gallai, kritikus kombinációi grafikonok pontosan grafikonok, amelyben minden egyes csatlakoztatott komponens egy kritikus tényező. Kiegészítés kritikus Count feltétlenül kritikus kombinációk, a tény, hogy Gallai annak bizonyítására, hogy alsó korlát a csúcsok száma kritikus.
Függetlenül attól, gráfelmélet, a koncepció a kritikusság faktor egy kiterjesztést matroidok meghatározzuk a fajta füllel bomlás matroidok. Matroid is kritikus tényező, ha ő a fül lebomlás, amelynek minden páratlan füle.