Véletlen szám generátor nagyobb kapacitású, savepearlharbor

Ebben a bejegyzésben megbeszéljük az alkalmazás egy lineáris kongruencia módszer pszeudo-véletlenszám bit mélység 64 bit és 128, ami megmagyarázza a működési elve és paraméterek kiválasztása.
Ha a terhet, hogy használja a RNG a standard könyvtár, akkor azt nem szabványos követelményeknek, vagy egyszerűen csak a vadászat, hogy ellenőrizzék a teljes folyamat véletlen szám generálás az alkalmazásban, akkor szívesen a vágás.
Le standard generátor!
Elég gyakori programozási nyelvben funkció generáló véletlenszerű (vagy rendkívül precíz, pszeudo) számokat. Néha azonban szükség van, hogy végre a saját véletlenszám-generátor (RNG). Bár RNG „out of the box” általában elég jó, hogy használja a legtöbb esetben, de az is előfordul, hogy túl meredek a generátor, mint ez nem szükséges, de a beépített RNG még mindig nem tetszik.
Az okok különbözőek lehetnek, és nem nyilvánvaló első pillantásra. Először is meg kell jegyezni, hogy a probléma a véletlen szám generálás gyakran magában megtalálni az egyensúlyt a sebesség és a minőségi eredményeket. Néha meg kell, hogy egy kicsit gyorsabb, vagy egy kicsit bonyolultabb.
Másodszor, RNG - nem csak a rendetlenség az aritmetikai műveletek, és szigorúan determinisztikus algoritmus, amelynek jellemzői igen eltérőek lehetnek. Egyes tudományos kísérletek szükségesek, hogy teljes mértékben leírja a feltételeket vizsgálatokat annak érdekében, hogy biztosítsa a lehetőséget reprodukálása. Ez magában foglalja egy algoritmus és paramétereit RNG. Ebben az esetben jobb, ha a végrehajtás.
Lehet, hogy egy probléma, amely szükséges az egyidejű működése különböző RNG. Ez más, és a beépített generátor általában egy. Akkor biztosan több példányban futtatni a különböző kiindulási gabona, de ebben az esetben a generátor ad tagjai ugyanabban a sorrendben (amely ciklikusan ismétlődik) egyszerűen kezdve különböző helyeken. ciklus hossza óriási, de elméletileg problémákat okozhat.
Az én esetemben, szükséges volt, hogy létrehoz egy 128 bites szám. A C ++ van egy funkciója, amelyek legalább 64 bites. Miután hosszas gugleniya találtam zavart rand () és RAND_MAX közé fog esni a különböző fordítóprogramok, mankók állítva generálni 64 bit, és úgy döntött, hogy felhagy a beépített RNG. Írásban a generátor tűnt elemi feladat - egy pár ismétléseket lineáris egybevágó generátor, hogy két 64 bites számokat, majd ragasszuk össze őket. Nem volt olyan könnyű. De kezdjük az elején.
Tehát folytassa a létrehozását a RNG. Ennek alapján vesszük a legegyszerűbb és legnépszerűbb lineáris kongruencia generátor, hogy működik az alábbi képlet szerint:
ahol xi. xi + 1 - a jelenlegi és a következő véletlen szám; a. c és m - állandók; mod - üzemeltető megtalálni a fennmaradó részlege.
A konstans m gyakran venni, hogy 2 32, illetve 2 64 elkerülése részlege szoftveres megvalósítása. Amelyek eredményeként kapott 64 bites maradványokat, szoktam m = 2 64. De hol kap egy állandó és c. A Wikipedia, a következő pár találtuk: a = c = 6364136223846793005 és 1442695040888963407. Gondolkodás nélkül írtam egy generátor segítségével ezeket a paramétereket, és kezdett vizsgálatot a genetikus algoritmus. Hamarosan azonban fixate. A gyanú esett az RNG. Kiderült, hogy több LSB a kapott egyenként 64 bites „random” szám bizonyítani nem véletlen viselkedést. Az értékek néhány bit egymást követő számok jelennek monokróm képek:


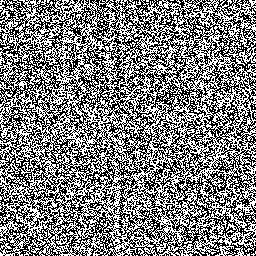
Alacsonyabb értékekkel 5-én, 15-én és 20-án bitek (számozott nulla)
Körülbelül 20-24 LSB nem alkalmas. A növekvő számú mentesítés növeli az esélyét. Így, így egy 64-bites véletlen szám, két lineáris kongruencia generátor iteráció van szükség. Az eredmény az összefűzés két 32-bites fragmentumok:
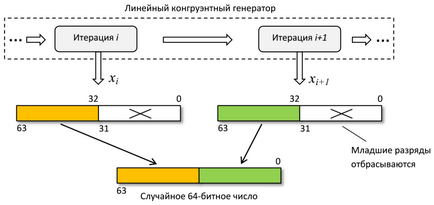
Például java.util.Random használja ugyanazt az elvet, de annak a ténynek köszönhető, hogy a m = 48. 2 ott eldobjuk LSB 16 csak hosszú int és generáció. Ez természetesen negatívan befolyásolja a minőségi véletlen számokat.
Itt látható egy példa a 64-bites sorszámokat, amelyet úgy kapunk, ha a = 6364136223846793005, c = 1442695040888963407, m = 2 64. X0 = 0 ábrán leírtak módon:
1442695037175000593
11166244415259155177
7076646891078057782
1459328390042580878
8905969149530007863
11682375496967736740
897247724006084730
Hogy véletlen ezek a számok? Körülbelül szintjén az RNG a szabványos Java könyvtár, talán még egy kicsit jobban. A számítás az egyes szám csupán két szorzásra.
Ha szüksége van több különböző oszcillátorok, meg kell választani a többi érték az állandók a, és c. számított m = 2 64. A cikk ennek referencia példákat mutat a három állandók a „jó minőségű”:
c - páratlan, m = 2 64