Lecke - meghatározása származék

Rövid leírása a dokumentum:

A következő példa megvizsgálja a kérelmet, a koncepció az származéka döntése geometriai problémákat. Ehhez először nyilvánosságra a koncepció egy érintőleges. A koordinátasík képviseli függvényében grafikonon jelölt két pontot M és S vezetéken keresztül jelölt pontot végezzük. Azt mutatja, hogy az S pont közeledik M. pontjával összekötő egyenes helyzetben megközelíti a helyzetét érintő ponton M. hogy is érintő jelentése határpozíciója szelő két ponton át során keletkezett megközelítés pontokat. Miután fogalmának bevezetésével érintő tekinthető érintő a grafikon y = f (x) a M pont (a, f (a)). Meg kell találni a sarokba érintőleges együttható. Erre a célra, bizonyos távolságra a jelölt pont M N (a + SH, f (a + NMR SH)). Egyenes meredeksége a tangens a szög, amelynél fekszik tartalmazó sort a háromszög átfogója által alkotott növekmény az érvelés és ðH Au növekmény funkciót. Ennek megfelelően, a sarokban vágási együtthatót adja ksek. = Au / SH. Amikor közeledik pont SH → 0. Nyilvánvaló, hogy a megközelítési az érintési pontok meghatározott végállás szelő meg SH → 0 kkas. = Lim ksek. vagy kkas. = lim Au / SH.

Következtetések jellemzője a matematikai modell megoldása mindkét problémát feljegyzések formájában meghatározása differenciálhányados, annak megállapítása, amely megjelenik a problémákat. Megjegyezzük, hogy egy függvény y = f (x), meghatározott ponton x és annak szomszédságában, a határérték Au / ðH át ðH → 0 a származéka y = f (x) ezen a ponton. Bemutatjuk a jelölést a származék f „(x). Az abszorpciós anyagot olyan származékának tekinthető egy lineáris függvény - Megjegyezzük, hogy mivel a korábban találtak a függvény az y = kx + m Lim limit Au / S H a H = k → 0, y '= (kx + m)' = k. Továbbá, a talált korlátozó funkció y = x 3. egyenlő Lim Au / H = 3x 2 át ðH 0 → azt jelenti, hogy a származék y „= (x 3) = 3 2.

Ebből kiderül, a fizikai és geometriai jelentése a származék. Megjegyezzük, hogy a fizikai értelemben törvény egyenes vonalú mozgás s (t) a származék a pillanatnyi sebesség v = s'(t). A geometriai értelemben egy érintő. végzett x = a, hogy a grafikon y = f (x) a származékot f „(a) - a lejtőn a tangens.

Figyelembe véve a jelentése a-származék és annak képletű megtalálásához Lim Au / H = f „(x) SH → 0, akkor majdnem közvetlenül arányos a növekmény funkciója a növekmény a érv az együttható képviselő származékot δu≈f” (x) · ÕH. Így, a függvény deriváltját y = x 3 δu≈3h igaz aránya 2 · ðH.

Egy algoritmust differenciálhányados, amely köteles:

• A keresést a pont x f (x);
• Az átmenet a pont x + S H találni f (x + S H);
• Find a növekmény az f (x + NMR SH) - f (x);
• Készítsen arány Au / SH;
• Find lim Au / ðH át SH → 0, vagyis az F „(x).

Szerint ez az algoritmus látható példa a kimutatási differenciálhányados f (x) = C, ahol a (C) = 0; f (x) = 1 / x, ahol (1 / x) = - 1 / x 2.

Az az elképzelés, differenciálódása funkciókat, hogy van, megtalálja a származék. Meg kell jegyezni, hogy a függvény differenciálható egy pontban, ha van benne egy származéka, és differenciálható függvény egy ponton a folytonosságát, és az ellenkezője nem igaz. Megerősítve jóváhagyása ez a példa az, hogy megtaláljuk a származék x pontban = 0 a függvény az y = | x |. Meg kell jegyezni, hogy annak ellenére, a folytonosság a függvény ezen a ponton, akkor az érintő az ütemezés nem lehet ott. És ez azt jelenti, és van ezen a ponton a származék. Ezt a következtetést a képernyőn megjelenő külön ajánlott tárolási. Egy példa az elfogadás a függvény y = f (x), ahol X<0 равна -√-х, а на промежутке x>= 0 egyenlő √h. Az ábrán ábrázoltuk függvényt, ahol a folyamatos, jól látható. Azonban, az x = 0 érintő a gráf nem épül, ezért ezen a ponton nincs-származék. Emlékeztetett arra, hogy ha egy bizonyos ponton a grafikon az érintő nem építhető, vagy merőleges az X-tengely, a nem-differenciálható függvény. Ebben a példában, differenciálható függvény. Önkényes gráf egy példa az utóbbi úgy vélik differenciálhatósági a három pontot.

Vegyünk két különböző feladatokat, fizikai és geometriai, amelyben mindkét kialakulásához vezet egy új matematikai modellt.

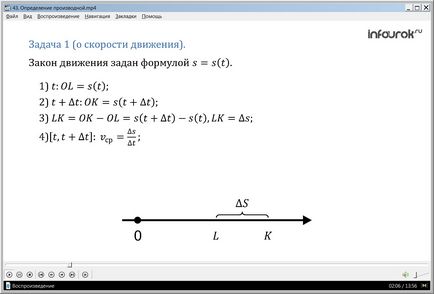
1. feladat (a jármű sebességét). Szerint a vonalat, amelyen vannak beállítva a referenciapontot, az egység (mérő) és iránya, egy mozgó test (anyagi pont). A törvény mozgás képlettel definiált s = s (t) (ES egyenlő ES TE), ahol t - idő (másodperc), s (t) - helyzetben a test az egyenes vonal (koordináta mozgó anyagi pont) t időpontban képest a felső referencia (méterben). Find test sebessége t időpontban (m / s).

Határozat. Tegyük fel, hogy t időpontban a szervezetben pontban

L (ábra. 1), az emelkedő elejétől mozgásának OL = s (t). Adjunk az érv t

növekmény dt (delta TE), és megvizsgálja a t + dt időpontban. Koordináta anyagi pont lett egy másik test ezen a ponton van azon a ponton, K: OK = s (t + t) (egyenlő mintegy ka es TE TE plusz delta).

Tehát, t másodpercig test mozgott a pont L pont K, azaz LK telt módon. Van: LK = OK-OL = s (t + t) -S (t). A kapott különbség azt elemzi növekmény funkció: s (t + t) -S (t) = s. Tehát, LK = s (m).

Path s (méter) karosszéria tartott t másodperc alatt. Ez könnyű megtalálni az átlagos sebesség a mozgás során az időintervallum [t, t + t]: VaV. = (M / s) (az átlagos sebesség egyenlő a relatív delta es TE delta).

Mi az a sebesség, v (t) a t időpontban (néha a pillanatnyi sebesség). Azt mondhatjuk, hogy ez az az átlagos sebesség egy időköz alatt [t, t + t], azzal a megkötéssel, hogy t értéke kevésbé van kiválasztva; más szóval, azzal a megkötéssel, hogy a T0. Ez azt jelenti, hogy

v (t) = (Ve a te határa megegyezik az átlagos sebesség), és a

Összefoglalva a probléma megoldásának 1, megkapjuk:

Annak érdekében, hogy megoldja a következő problémát, meg kell, hogy megtudja, mit értünk érintő a görbe.

Dana L görbe (. Ábra 2) ellátva kiválasztott pont M. Veszünk egy másik pont a görbén, és elegendően közel M, - az a pont S.

Rajzolj egy átkelés MS. Következő fogjuk zoom S pont a görbén L

M pontban pásztázóegysége MS megváltoztatja a pozícióját, úgy tűnik, hogy elforgatható pont körül M. Gyakran előfordul, hogy megtalálható a folyamat sorban, amely egy bizonyos korlátozó helyzetében a szelő; ez egyenes - a végső pozícióját a világos - az úgynevezett

L érintője ponton kapott görbét M.

2. feladat (o érintőleges a grafikon). Dan grafikon y = f (x). Kiválasztott az M pont (a, f (a)) (um koordinálja és Aeff egy). Ezen a ponton a grafikonon az érintők (feltételezzük, hogy létezik).

Keresse az érintő meredeksége.

Határozat. Adunk érv növekmény x és megvizsgálja a grafikon (3.), A pontot az abszcissza N a + x. Az ordináta a pont N egyenlő f (a + x). A lejtőn a szelő MN. azaz közötti szög az érintő és a szelő x tengellyel. Ez képlettel számítjuk ki (Ka egyenlő szekáns delta y osztva Delta X).

Ha most hagyjuk x nullára, a lényeg N a görbe kezd megközelíteni a ponton M. tangens jellemeztük

mivel a korlátozó helyzetében a szelő ezzel a közelítés. Ennélfogva, természetesen feltételezzük, hogy a sarok érintője kkac arányt a következő képlet alapján számítható (Ka Ka érintő egyenlő limit szekáns).

A képlet ksek fenti. kapjuk (ka tangens egyenlő limit delta y osztva Delta X, Delta X nullához).

Összefoglalni. A folyamat során a megoldására két problémát jöttünk ugyanazt a matematikai modell - a határ aránya a növekmény funkció a növekmény az az érv, ahol ez az érv növekmény nullához.

Nézzük meg, mi a határ az arány a növekmény funkció a növekmény az érvelés.

2. Meghatározás A származtatott

Definíció 1. Legyen a függvény az y = f (x) határozzuk meg egy adott x pontban egy bizonyos környéken. Adunk az érv x növekménye x, oly módon, hogy nem hagyja el ezen a környéken. Megtaláljuk a megfelelő növekmény Au funkciók és kompozíciós arányt. Ha a határérték ez az arány, feltéve x0, akkor ezt a határértéket az úgynevezett függvény deriváltját y = f (x) az x és jelöljük f „(x) (EHA bar X).

Így (a határértéket a delta y osztva Delta X egyenlő EF bar X).

Ahhoz, hogy kijelöl egy származékot gyakran használják jellegű”. (Y bar)

Megjegyezzük, hogy az y „= f” (x) (y bár ef bar X) - egy új funkció, de társított az y = f (x), meghatározott összes ilyen pont x, ahol van a kimutathatósági határ felett . Ezt a funkciót nevezzük a következőképpen: a függvény deriváltját y = f (x).

Egy példa a lineáris függvény az y = kx + m egyenlőség.

Ez azt jelenti, hogy az y „= k vagy több,

Bebizonyítottuk, hogy az y = x 3 egyenlőség

Ez azt jelenti, hogy az y = 3x 2 vagy több, (X 3) = 3 2. (X kockázott bar X egyenlő három a másodfokú)

Származtatott a fizikai és geometriai szempontból.

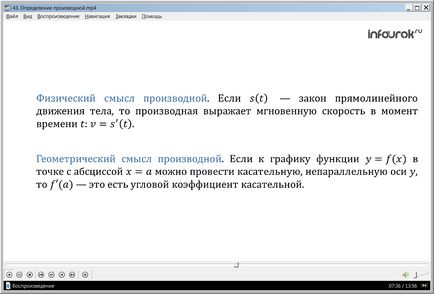
Fizikai (mechanikai) értelmében a származék a következő. Ha s (t) - a törvény egyenes vonalú mozgás a test, majd ezt a származékot kifejezi a pillanatnyi sebesség t időpontban:

v = s'(t) (ve egyenlő lökete TE ES).

Geometriai értelmében a származék a következő. Ha a függvény grafikonját y = f (x) a ponton az abszcissza, x = a tehető érintőjének nem párhuzamos az Y tengelyen, f „(a) van egy tangenciális szögletes együtthatót.

Tegyük fel, hogy a függvény az y = f (x) a származék egy adott x pontban (határa az arány a növekmény a növekmény az érvelés funkció differenciálhányados).

Kielégítően kis környezetében x közelítő egyenlet érvényes: (az arány a lépésekben, hogy a növekmény az érvelés funkció megközelítőleg egyenlő a származékot funkció), vagy

y f „(x) · x. (Funkció növekmény megközelítőleg egyenlő differenciálhányados szorozva a növekmény az érvelés).

Lépésköz funkció „közel arányos”, hogy a növekmény az érvelés, az arányossági tényező a derivált érték (egy adott x pontban). Például, a függvény az y = x 3 következő közelítő egyenlet y 2 · x 3

Megfogalmazzuk az algoritmus megtalálásához származék.

Egy algoritmust találni származékai (az y = f (x))

1. A fix x értékét, meg f (x).

2. Add meg az érvelés x lépésekben, menjünk át egy új helyre

x + x, megtalálása f (x + x).

3. Find a növekmény funkció: y = f (x + x) -f (x).

4. Készítsen arány.

5. Számítsa limit.

Ez a határérték f „(x).

1. példa Find a származékot egy konstans függvény y = S.

Határozat. Az általunk használt algoritmust találni a származék.

1) A rögzített x érték, van: f (x) = C

2) azon a ponton x + x van: f (x + x) = C

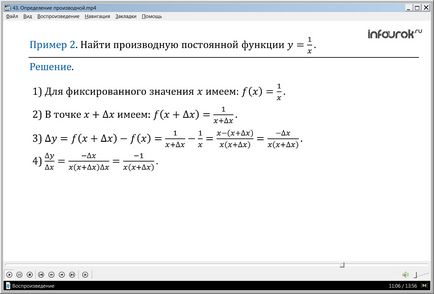
2. példa Find a függvény deriváltját y =.

Határozat. Az általunk használt algoritmust találni a származék.

Ha a függvény az y = f (x) a származék x pontban, akkor az úgynevezett differenciálható ponton x. A derivált függvény y = f (x) nevezzük származtatás függvény az y = f (x).

Ha a függvény differenciálható egy pontban x, akkor folyamatos ezen a ponton.

Az ellenkezője nem igaz.

Néhány példa: a funkció y = | x | mindenütt folyamatos és az x = 0 (4. ábra), de a tangens, hogy a grafikon a „kapcsolódási pont” (0, 0) nem létezik.

Ha valamikor a függvény grafikonját nem húzhat egy érintő, akkor ezen a ponton nincs-származék.

Példa. Ábra. Az 5. ábra egy grafikon, egy darabonkénti függvény az y = f (x), ahol a

A függvény folytonos az egész számegyenesen, beleértve azon a ponton, x = 0. És érintő a függvény grafikonját létezik sehol, beleértve az x = 0. De azon a ponton, x = 0 az érintő egybeesik a y tengely, azaz a merőleges az abszcissza, annak egyenlet az x = 0.Takaya sorban nincs meredeksége, azonban, nem létezik, és F „(0).

Ütemezett kötni a differenciálható függvények, akkor ellenőrizni kell, hogy lehetséges-e egy bizonyos ponton, hogy dolgozzon egy érintőleges függvény grafikonját, nem merőleges az x tengely. Ha lehetséges, akkor ezen a ponton differenciálható függvény. Ha egy bizonyos ponton érintő a grafikon a funkció nem létezik, vagy hogy merőleges legyen az x-tengely, akkor ezen a ponton differenciálható függvény. Így szerint a grafikon a ábrán látható. 6, arra lehet következtetni, hogy a függvény folytonos mindenütt, kivéve a ponton x = a; függvény differenciálható mindenütt, kivéve a pontok x = a és x = b - nem létezik egy érintő, amelyben x = ITT érintője párhuzamos az y tengellyel.