Kulish Ljudmila matematika tanár doshas №111g
Donyeck regionális irodája MAN Ukrajna
Donyeck Tankönyvek I-ІІІstupeney №111
Fizikai és matematikai és gazdasági osztály
Szakasz: Applied Mathematics
Panasiuk Vaszilij Anatolievich
Donyeck általános iskola №111
Ljudmila Kulish
DOSH №111 matematika tanár
Annak szükségességét, tört számok az eredménye gyakorlati emberi tevékenység. Meg kell találni a készülék részesedése őseink jött egy részlege a zsákmány után a vadászat. A második jelentős oka tört számok kell tekinteni, mint a mérési értéket a kiválasztott mértékegységet.
Az első frakció, amely az emberek találkoztak. Ez volt a fele. Bár a nevét, minden ezen frakciók nevéhez való nevezők (három - „harmadik”, négy - „negyed”, stb ...), így a fele nem - a neve minden nyelven semmi köze a „két”. A következő lövés volt a harmadik.
Így. az első lövés, amely bemutatja, hogy a történet, ez egy töredéke a forma - - az úgynevezett egységes frakció vagy részletét (a latin aliquot -. «Néhány»).
Az egyes frakciókat találhatók a legrégebbi fennmaradt matematikai szövegek, amely több mint 5000 évvel ezelőtt - az ókori egyiptomi papirusz és babiloni ékírásos táblákat. Egyiptomi frakció - matematikai összege több frakciójának formájában (úgynevezett aliquot frakciók). Más szóval, minden frakció egy számláló értékét. egyenlő egy és a nevező. Ez jelenti a természetes szám.
Egyiptomi frakció egy pozitív racionális szám formájában; Például, az egyiptomi frakciót. írva a fenti lehet írva, mint egy frakciót 43/48. Meg lehet mutatni, hogy minden pozitív racionális szám is képviselteti formájában egyiptomi frakció. Összege által használt típusú matematikus. mivel a meghatározás frakciók kezdve az időben az ókori Egyiptom a középkorban.
Feladatokat döntés aliquot frakciókat alkotnak széles osztályát nem szabványos feladatokat. Ezek közé tartoznak különösen az összes feladatot, amit meg szeretne osztani bármelyik vagy források több részre a legkevesebb akció erre a célra.
célkitűzés:
Ahhoz, hogy megtudja, milyen fontos a alikvot frakció életünk
Kutatási célok:
Tanulni eredetét aliquot frakciók.
Tekintsük az alap működését az aliquot frakciók.
Fordítsuk és a problémák megoldása a gyakorlati tartalmat.
2. törzsanyag.
Eredeti aliquot frakciók.

A téma a „aliquot frakciók” egy érdekes téma, hogy tanulmányozza frakciók. Szembesülve ezt a kifejezést először, érti, hogy miért az ókori Egyiptomban Matematika „igazi” hittem csak frakciók aliquot frakciók.
Tehát mind az egyiptomiak frakciót elszámolni az összeget a részvények. azaz frakciókat formájában 1 / n. Például: 8/15 = 1/3 + 1/5. A frakciót 1 / n. (Ahol n - természetes szám), amely az egyiptomiak kedvelt modern matematika nevű alikvotokat (a latin aliguot- „néhány»«), amely a frakciók részleteit a tört számlálója említett 1. És még az aliquot frakciók gyakran kívánta bemutatni összegeként kisebb aliquot frakciók. például,
Ezeket a frakciókat együtt használjuk egyéb felvétel az egyiptomi frakciókat osztani „Hekaté,” a nagy részét az intézkedés az ókori Egyiptom, t.e.alikvotnye frakciót egyiptomiak szükséges gyakorlati célokra.
Hadd illusztráljam ezt egy példával. Tekintsük a következő probléma: „7. § kenyereket között 8 fő.”
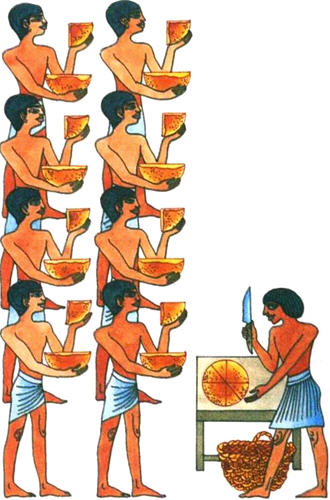
Nyilvánvalóan. mindenki kap egy cipót. A modern diák volna valószínűleg megoldotta a problémát így: meg kell vágni minden kenyeret 8 egyenlő részre, és így minden egyes ember egyik oldalára kenyeret. És itt van, hogy ez a probléma megoldódott a Rhind papirusz - ókori egyiptomi matematikai szöveg átírása 1650 BC Ahmesom írástudó.
Mert. Ezért minden személynek biztosítani kell a fél, negyed és nyolcad kenyeret. Most már világos, hogy a szükséges 4 kenyér felére csökken, 2 kenyér 4 darab, és csak egy kenyeret - 8 rész. És ha a hallgató volna, hogy 49 vágások, a Ahmesu - összesen 17, azaz Egyiptomi módszer majdnem 3-szor gazdaságosabb.
Ha vágott minden a 8 szelet kenyér, kellett volna költeni 49 darabok. És az egyiptomi ez a probléma megoldódott a következő: 7/8 = 1/2 +1/4 +1/8. Ez azt jelenti, hogy minden egyes ember ad polhleba. kenyér és egy negyed uncia kenyeret. Majd meg kell tennie majdnem háromszor kisebb bemetszést.
Egyiptomi frakció továbbra is használtak az ókori Görögországban és később matematikusok a világ minden tájáról, hogy a középkorban, annak ellenére, hogy a hozzászólások hozzá az ókori matematikusok. Például, Claudius Ptolemaiosz mondott a kényelmetlenséget a használó egyiptomi frakciók összehasonlítása a babiloni rendszer (pozicionális számrendszer)
Fontos munka a tanulmány egyiptomi frakciók matematikus Fibonacci a XIII században című művében «Liber Abaci» - Ezen számítás alkalmazásával tizedessel és a hétköznapi frakciói kiszorította végül egyiptomi frakció. Fibonacci használt bonyolult felvételi frakciókat, melyek között szerepelt rekordszámok vegyes alap és rekord összegeiként frakciók, és gyakran használják egyiptomi frakció. Szintén a könyvben kaptak fordítás algoritmusait rendes frakciók Egyiptomban.
2.2 Alapvető műveletek aliquot frakciók
Elképzelni, hogy milyen szám összegeként aliquot frakciók, néha meg kell gyakorolni. ritka találékonyság. Például, a számot 2/43 a következőképpen fejezhető ki: 2/43 = 1/42 +1/86 +1/129 + 1 / 301.Proizvodit aritmetikai műveleteket számok, megjelenítését az összege egységet frakciók, nagyon kellemetlen.
Ezért, a folyamat problémák megoldására a bomlása aliquot frakciók, mint az összege kisebb aliquot frakciók az az ötlete támadt, hogy rendszerezése a bomlás frakciók, mint egy képlet. Ez a képlet érvényes, ha azt akarjuk, a bomlás egy aliquot részt a frakció két alikvot a frakció.
A képlet a következő:
Példák frakciókból bomlás:
De ha átalakítják formula, megkapjuk az alábbi hasznos egyenlőség:
Ie alikvot frakció képviselik a különbség a két aliquot frakciók, vagy a különbség a két alikvot amelynek nevezők a egymást követő számok egyenlő a termék.
Térjünk vissza a képlet és ezt bizonyítani egyenletet:
(N + 1) / ((n + 1) * n) a vágás után megkapjuk
Tehát kiderül, hogy az 1 / n = 1 / n. Ez a formula igaz.
De megy tovább, és az alapján a különbség aliquot frakciók megoldásához, látszólag megoldhatatlan problémát jelent az átlagember:
Mi használja a képlet a bomlás egy aliquot részt a frakció formájában a különbség:
1/20 = 1 / (4 * 5) = 1 / 4-1 / 5, stb
Behelyettesítve már megállapított kifejezést a példánkban, ezt kapjuk:
Mi már bemutatott egy képlet, mint a könnyű bomlása egy alikvot frakciót 2 kifejezések. Amikor a bomlás 1 két komponenseket kapjuk:
1 = 1/2 + 1/2 (A képlet érvényes!). Ahhoz, hogy bomlanak 1-3 szempontjából. veszünk egy lövés, és egy aliquot képletű kibontásához két aliquot a frakció:
Osztható 4 szempontjából. osztani egy másik lövés két aliquot a frakció:
Ami a 5: 1/6 = 1/7 + 1/42 => 1 = 1/2 + 1/4 + 1/12 + 1/7 + 1/42.
2.3.1.Predstavit száma 1 összegeiként frakciók különböző aliquot
A) A három kifejezés
B) négy kifejezések
Ahhoz, hogy tudjuk, milyen év Donyeck lesz az európai labdarúgó bajnokság szükséges mennyiségű aliquot frakciók
Így. fejlődésének ez a téma, megtanultuk, hogy az első frakciókat, ami működött az emberek alikvot a frakció. Azt találtuk, hogy egyes racionális szám formájában a / b bontható egyes frakciók.
Problémák felhasználásával aliquot frakciók tartalmaznak széles osztálya nem szabványos feladatok. Aliquot frakciókat használni, ha akarsz valamit, hogy több részre oszlik, a legkevesebb akció erre a célra.
Bomlása a frakciók két alikvot frakciókat rendszerezett, mint egy általános képletű. konvertáló, hogy könnyű eldönteni Diákolimpia matematikai problémák az évek során.
Miután megoldotta a problémát a bomlás aliquot frakciók két aliquot frakciók, már arra a következtetésre jutott, hogy a bővítés három, négy, öt, stb aliquot frakciók állíthatók elő bővülő egyik kifejezések két frakcióra, a következő kifejezés két aliquot frakciókat, stb
Így. Aiiquot frakciókat (amelyben a számláló 1) hosszú ideig voltak az egyedüli frakciókat. ami valahogy tudott működni az emberek, és a cselekvés szabályok önkényes frakciók kifejlesztett „viszonylag új keletű”.
A modern matematika helyett egyiptomi frakciókra frakciók, tizedes. de egyiptomi frakció is tovább kell tanulmányozni a számelmélet és a matematika történetében.
A jövőben szeretnék kutatni alikvotokban szétválás, és megszorozva, úgy vélem, hogy egy aliquot mindig kapunk. És ez nyilvánvaló.