Bevezetés a topológia (a kannák és humán)
Nem emlékszem, mikor először hallottam a topológia, de én rögtön érdekel ez a tudomány. Maker válik a bagel, körének kifordítjuk. Sokan hallottak már róla. De azoknak, akik szeretnének mélyebbre témára egy komoly szinten, gyakran vannak nehézségek. Ez különösen érvényes a fejlesztés a legelemibb fogalmak, amelyek lényegében nagyon elvont. Sőt, sok forrásból, mintha kifejezetten törekszik, hogy megzavarja az olvasót. Mondjuk orosz wiki ad egy nagyon homályos megfogalmazás, amit a topológia. Azt mondja, hogy ez egy tudomány, amely tanulmányozza a topologikus tér. A cikket a topológiai tér az olvasó láthatja, hogy a topológiai tér - ezen a helyen fel van szerelve a topológia. Az ilyen magyarázatok stílusa lemovskih sepulek nem tisztázza a lényege a téma. Megpróbálom felvázolni további kulcsfontosságú alapfogalmakat tisztább formában. Az én feljegyzés nem fog fordulni kezdőknek és bagel, de az első lépés, hogy előbb-utóbb megtanulják ezt a mágiát.
Azonban, mivel nem vagyok matematikus, de a humanitárius száz százalékos, ez elég lehet, hogy az írásbeli alábbi - egy hazugság! Nos, vagy legalábbis annak egy részét.
Kezdjük egy rövid ismétlés halmazelmélet. Azt hiszem, a legtöbb olvasó is ismeri, de mégis felidézni az alapokat.
Tehát, úgy vélik, hogy a definíció sokasága Nem, és hogy ösztönösen érti, mi ez. Kantor azt mondta: „A” többszörös „alatt azt értjük, hogy a vegyület bizonyos egész M egyes jól elkülöníthető tárgyakat m Intuíciónk vagy gondolatunk (amelyet a továbbiakban” elemek „a készlet M)”. Természetesen ez csak egy ábrás leírását, nem egy matematikai definíciója.
Halmazelmélet ismert (bocsásd meg a szójáték) sok csodálatos paradoxonok. Például. Mivel is jár matematika válság elején XX-ik században.
A készletek végesek.

Vannak végtelen. Például az egész számok, amely betűvel jelöljük ℤ (vagy csak a Z, ha van egy billentyűzeten nincs göndör betű).

Végül, van egy üres halmaz. Ez pontosan egy az egész univerzumban. Van egy egyszerű igazolás ezt a tényt, de nem adom meg itt.

Ha a beállított végtelen, akkor megszámlálható. Számlálás - a készletek, amelynek elemei sorolható természetes számokkal. A nagyon természetes számok halmaza, ahogy kitalálta, megszámlálható. És itt van, hogyan lehet számozni az egész.
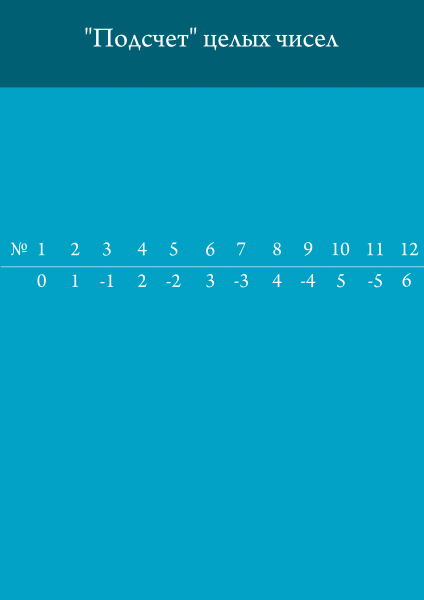
A racionális számok nehezebb, de így a számozás. Ezt a módszert nevezik átlós eljárás, és úgy néz ki, mint az alábbi képen.
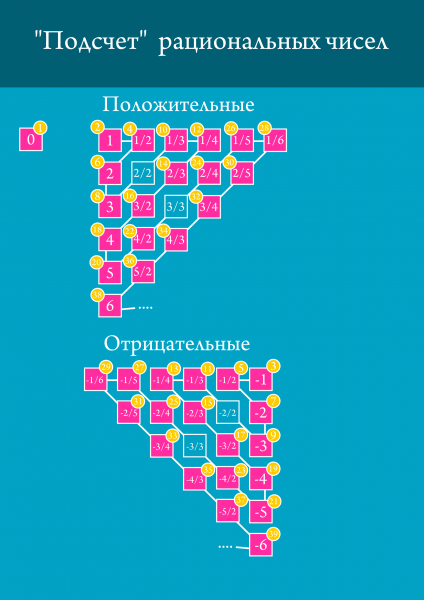
Mi cikcakk lépés racionális számok 1-től kezdődően így mindegyik számot, amely már kapott hozzárendelésével páros. Negatív racionális számokat tekintjük, ugyanúgy, csak a páratlan számok, kezdve 3. Zero hagyományosan megkapta az első számot. Így látható, hogy minden racionális számokat lehet számozni. Minden szám, mint 4,87592692976340586068 vagy 1,00000000000001, vagy -9092, vagy akár 42 kap a szám ebben a táblázatban. Azonban ez a rangsor nem az összes számot. Például V2 nem fog szoba. Ha valami nagyon csalódott görögök. Azt mondják, az a srác, aki felfedezte az irracionális számok, megfulladt.
Általánosítása a koncepció a méret beállítása hatalom. Power of véges halmazok egyenlő a tagjaik számáról. Teljesítmény végtelen halmazok jelöli a héber betű aleph index. A legkisebb végtelen erő az az erő ℵ0. Ez egyenlő a hatalom megszámlálható halmazok. Mint látható, ezért a természetes számok, annyi, mint egész vagy racionális. Furcsa, de igaz. Next - számossága a kontinuum. Jelezte ℵ1. Ez az erő a valós számok halmaza ℝ, például. Van egy hipotézist, hogy a számossága a kontinuum és a teljesítmény aleph-1-1 és ugyanaz. Ie hogy nincs köztes hálózati méz megszámlálható halmazok és a kontinuum.
A készlet lehet műveleteket végezni, és szerezzen új készletek.
1. A készlet lehet kombinálni.

2. A halmazok „kivonjuk”. Ez a művelet a kiegészítés.

3. Kereshet a kereszteződésekben a készletek.
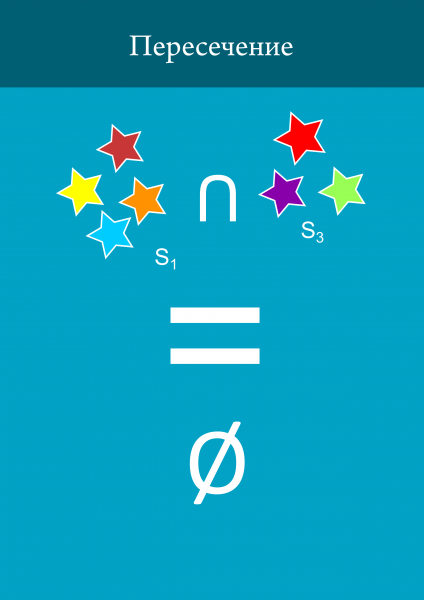
Tulajdonképpen ez az egész a készletek, meg kell tudni céljából ezt a cikket. Most folytassa a topológia is.
Topológia - a tudomány, hogy a tanulmányok a készlet egy bizonyos struktúrát. Ez a szerkezet is hívják topológia.
Tegyük fel, hogy van egy nem üres halmaz S.
Legyen ez a halmaz lehet egy bizonyos szerkezetű, amelynek leírása sokasága, amely nevezünk T. T egy több részcsoportja a készlet S, oly módon, hogy:
1. Szükségtelen S és ∅ tartoznak T.
2. Az egyesület önkényes családok elem T tartozik T.
3. A metszéspontja egy tetszőleges véges elem T családjába tartozik T.
Ha ez a három tételek teljesülnek, a szerkezet a mi topológia T az a beállított S. A halmaz elemeit T úgynevezett nyitott készlet S a topológia T. Komplement nyitott halmazok zárt halmazok. Fontos megjegyezni, hogy ha a beállított nyitva van, ez nem jelenti azt, hogy nincs lezárva, és fordítva. Ráadásul ebben a topológia képest némi készlet lehet egy részhalmaza, amelyek sem nyílt, sem zárt.
Itt egy példa. Tegyük fel, hogy van egy sor, amely három színű háromszög.

A legegyszerűbb topológia rajta az úgynevezett tapintatlan topológia. Itt is van.

Ez a topológia is nevezik topológia agglomerált pont. Ez egy nagyon meghatározott, és az üres halmaz. Ez tényleg megfelel axiómák topológia.
Egy készlet, megadhatja több topológia. Itt van egy másik nagyon kezdetleges topológia, hogy van. Ez az úgynevezett diszkrét. Ez a topológia, amely minden alcsoportjánál egy adott készlet.

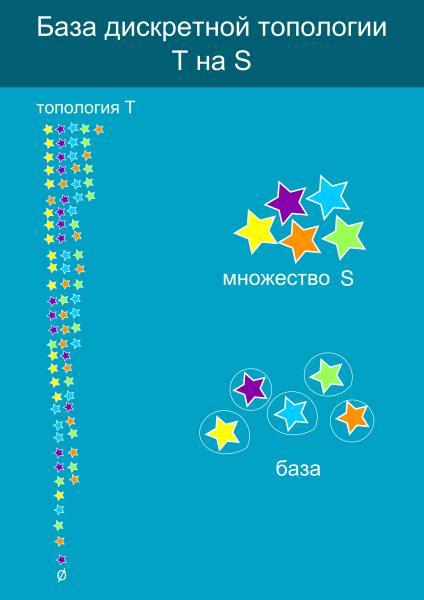
És itt egy másik topológia. Ez meg a készlet több színű csillagok 7 S, amit felvázolt leveleket. Győződjön meg arról, hogy ez a topológia. Nem vagyok biztos benne, hirtelen kihagyott néhány unió vagy kereszteződést. Ebben a képet kell tűzte S, üres halmaz kereszteződést, és az unió összes többi eleme a topológia is kell lennie a képen.

Egy pár topológia, és állítsa be, amely be van állítva az úgynevezett topológiai térben.
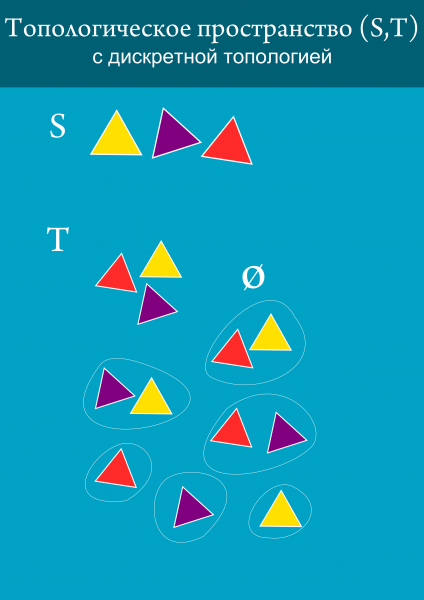
Ha a beállított sok pontot (nem beszélve arról, hogy lehetnek végtelen számú), majd felsorolja az összes nyitott szett problémás lehet. Például a diszkrét topológia a sor a három elem szükséges ahhoz, hogy egy listát a 8 meghatározza. A 4-elemkészlet fog tartalmazni diszkrét topológia 16, 5-32 6 -64, és így tovább. Annak érdekében, hogy ne felsorolni az összes nyitott készletek használjuk gyors-, hogy - kiírja az elemeket egyesület, amely biztosítja az összes nyitott készletek. Ez az úgynevezett alap topológia. Például a diszkrét topológia a három háromszög - ez lesz a három háromszög külön-külön, mert egyesíti őket, akkor kap az összes többi nyitott készlet ebben a topológia. Azt mondják, hogy az alap generál topológia. A készlet, mely elemeket generál adatbázist, az úgynevezett a talpat.
Az alábbiakban egy példát alapul a diszkrét topológia egy sor öt csillag. Mint látható, ebben az esetben, az alap áll, csak öt tagja van, míg több mint 32, a topológia részhalmaza. Ön vállalja, hogy a bázis, hogy leírja a topológia - sokkal kényelmesebb.
Melyek a nyitott szett? Bizonyos értelemben adnak egy ötlet „közelség” között a pontok és a különbség közöttük. Ha a pontok tartozhat két különböző nyílt halmazok, vagy ha olyan pont van a nyílt halmaz, amely nem a második, azok topológiai más. A tapintatlan topológia, minden pont ebben az értelemben nem lehet megkülönböztetni, mintha összeragadt. Éppen ellenkezőleg, a diszkrét topológia, minden pont a különbség.

Közötti kommunikáció nyílt halmaz és oktestnostyu lehet az alábbiak szerint történik. A nyílt meg - egy sor, amelyben minden elemnek van egy bizonyos környéken. Vagy fordítva, akkor azt mondják, hogy egy sor nyitott, ha ez egy szomszédságában minden pontjában.
Mindez a legalapvetőbb fogalmak topológia. Ezért még nem világos, hogyan kell csavarni a gömb belülről kifelé. Talán a jövőben képes leszek, hogy akár ilyen sorrendben (ha meg fogja érteni).