rugalmas erő, fizika
1. Megnyilvánulása rugalmas erők és a természet
Mint azt már tudjuk során a fizika alapvető iskola, a rugalmas erő járó alakváltozás a test, vagyis változtatják formájukat és (vagy) méretben.
Kapcsolatban áll a rugalmas alakváltozás a test erő nem mindig látható (a részleteket fogunk összpontosítani, hogy az alábbiakban). Emiatt a tulajdonságok a rugalmas erők vizsgálat általában egy rugó, az érthetőség kedvéért: a deformáció is jól látható, hogy a szem.
Felfüggesztése a rugóterhelés (ábra. 15.1, a). (Feltesszük, hogy a rugó tömegét figyelmen kívül lehet hagyni.) A rugó megnyúlik, vagyis deformált.
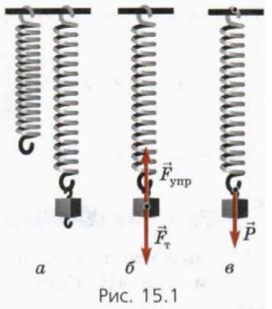
A felfüggesztett teher ható gravitációs m és alkalmazott a húzórugó ereje a rugalmas gyakorlat (ábra. 15.1, B). Ez okozta alakváltozás a tavasz.
Szerint a Newton harmadik a tavaszi oldalán terhelés hat, azonos nagyságú, de ellentétes irányú erőt (ábra. 15.1 in). Ez az erő - a teher súlya: ez az erő, amellyel a szervezet húzódik függőleges emelt (tavasszal).
Legyünk erőt és amellyel a rugót és kölcsönhatásban vannak egymással, össze vannak kötve Newton harmadik, és így azonos fizikai jellegű. Következésképpen a tömeg - ez túl rugalmas erőt. (Reagálás a tavasz oldalán terhelés rugóerő (terhelés súlya) miatt betölteni deformáció A deformáció nem észlelhető, ha a terhelés a súly vagy bár, akkor a terhelés, hogy egy hatalmas tavaszi betölteni törzs lett túl észrevehető: .. Látjuk, hogy kiterjeszti. ) erők rugóterhelés tömeg húzódik meg, hogy ez az oka annak deformációját. (A félreértések elkerülése végett, azt ismételten hangsúlyozni, hogy a tavasz, amelyre a teher fel van függesztve, nyúlik és nem alkalmazzák a rakomány a gravitációs erő a terhelés, és csatolni kell a rugó által a terhelés rugóerő (terhelés súly).)
Ebből a példából láthatjuk, hogy a rugalmas erő következménye és oka a rugalmas deformációja szervek:
- ha a test deformálódik, akkor a része ennek a test, a rugalmas erő (például, erő gyakorolja a 15.1 ábra, b);
- ha a test kíséretében a rugalmas erő révén (pl, hatályos 15.1 ábra a), ez a test deformálódik.
1. Melyik ábrán látható 15.1 Force
a) kioltják egymást, ha a terhelés a többi?
b) azonos fizikai természete?
c) kapcsolódnak Newton harmadik?
d) megszűnik egyenlő nagyságú, ha a terhelés fog mozogni gyorsulás, felfelé vagy lefelé?
Ez mindig látható alakváltozás a test? Mint mondtuk, „alattomos” funkció rugalmas erők, hogy a hozzá tartozó deformáció a test nem mindig látható.
Az alakváltozás a tábla súlya miatt feküdt rajta alma, az a szemnek láthatatlan (ábra. 15.2).
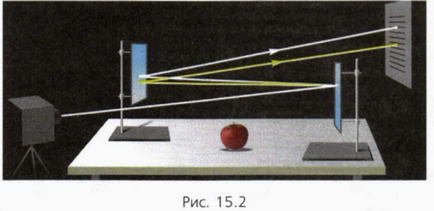
És mégis: csak azért, mert a rugalmas erő, amely felmerült eredményeként a deformáció az asztal, a birtokában egy almát! Deformáció az asztal lehet detektálni egy ötletes kísérlet. A 15.2 ábra A fehér vonalak vázlatosan jelzik a haladás, a fénysugár, ha nincs alma és sárga vonalak - során a fénysugár, ha az alma az asztalon.
2. Tekintsük 15.2 ábra, és magyarázza, hogy a deformáció a táblázat sikerült észrevehető.
Néhány veszély az, hogy nem veszi észre, a törzs, nem lehet látni, és a hozzá tartozó rugalmas erő!
Tehát szempontjából néhány problémába ütközünk „nem nyújtható menet.” Ilyen szavak azt jelentik, hogy csak elhanyagolható mennyiségű törzs menet (hossza növekszik), de lehetetlen, hogy elhanyagolja a rugalmas ható erők az izzószál, vagy az áram az izzószál. Tény, hogy „egyáltalán nem nyújtható szálak” no: pontos mérések azt mutatják, hogy minden szál egy kicsit, de feszített.
Például, ha a fenti kísérlet, egy csatlakoztatott terhelés egy rugó (lásd. Ábra. 15.1), cserélje ki a rugó „nyújthatatlan fonál”, akkor a súly alatt terhelés stretch fonal, bár annak deformációját, és lesz észrevehetetlen. És ezért jelen lesznek, és a fenti rugalmas erő. A szerepe a rugalmassága a rugóerő fog játszani a szálfeszítő erő irányította végig a menet.
3. Rajzok megfelelő 15.1 ábra (a, b, c), Rugócsere nyújthatatlan fonál. Jelölje meg a rajzokon ható erők a menet és a terhelés.
4. Két ember húzta ellentétes oldalán a kötél erővel 100 N minden.
a) Mi a feszítőerő a kötél?
b) hogy a kötélfeszítőelemként erő változás, ha az egyik végét kötve egy fa, és a másik végét húzza erővel 100 N?
Nature rugalmas erő
egy rugalmas erő miatt kölcsönhatása erők a részecskék, amelyek a test alkotja (atom vagy molekula). Amikor a test deformálódik (mérete megváltozik, vagy a forma), a távolságot a részecskék megváltozott. Következésképpen, a részecskék között, erőhatástól, hogy visszatérjen a testet deformálatlan állapotban. Ez az erő a rugalmasságát.
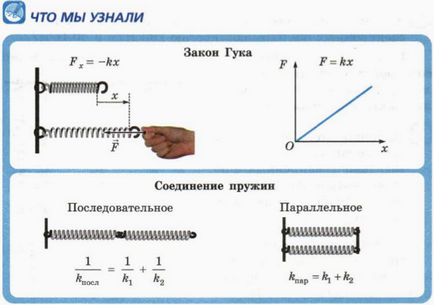
2. Hooke-törvény
Akkor felfüggesztjük a tavaszi azonos súlyú. Megjegyezzük, hogy a kiterjesztés egy rugó arányos a súlyok száma (ábra. 15.3).
Ez azt jelenti, hogy a deformáció a tavaszi arányos a rugalmas erő.
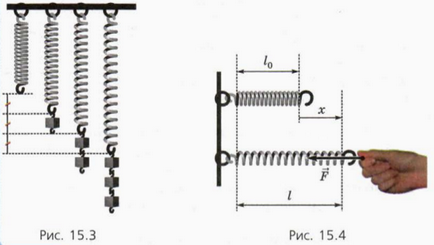
Jelöljük a deformáció (nyúlás) a rugó
ahol l - hossza a deformált rugók, és L0 - hossza nem deformált rugó (ábra 15.4.). Amikor a rugó megnyúlik, x> 0, és a nyúlvány által kifejtett rugalmas rugóerőt Fx <0. Следовательно,
A „mínusz” jel ebben a képletben emlékeztet arra, hogy alkalmazzák a deformált test rugalmas erő ellentétes irányú a deformáció a test: a megnyújtott rugó hajlamos tömöríteni, és tömör - szakaszon.
K együttható úgynevezett tavaszi állandó. A merevség függ a rugó anyagát, annak mérete és alakja. Egység merevítő 1 N / m.
(2) egyenlet az úgynevezett Hooke-törvény tiszteletére az angol fizikus Robert Hooke, aki felfedezte ezt a mintát. Hooke-törvény érvényes, nem túl magas alakváltozás (deformáció megengedett érték függ az anyag, amelyből a test készült).
(2) egyenlet azt mutatja, hogy a rugalmas erő F modul a modulhoz tartozó törzs arány x
Ebből a képletből következik, hogy a telek F (x) - a vonalszakasz áthaladó eredetű.
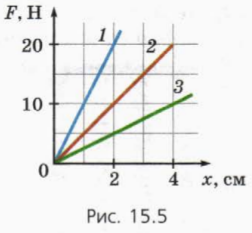
5. ábra 15.5 ábrázoltuk az elasztikus modulus elleni deformációs modulusa erőt a három forrás.
a) egy rugó merevségét a legnagyobb?
b) Mi a merevségét a legpuhább tavasz?
6. be egy súlyt kell függeszteni a rugóállandója 500 N / m, hogy tavasszal nyúlása egyenlő 3 cm?
Fontos különbséget tenni a tavaszi nyúlás x hossza l. A különbség a kettő között az alábbi képletekkel ábrázolt (1).
7. Amikor a rugó fel van függesztve egy 2 kg-os, a hossza 14 cm, és amikor felfüggesztik a súlya 4 kg, a rugó hossza 16 cm.
a) Mi a rugó állandó?
b) Milyen hosszú a deformált tavasz?
3. Egy vegyület, rugók
soros kapcsolás
Vegyünk egy rugó állandó k (Figure 15.6, a). Ha nyúlik erővel (ábra. 15.6 b), a nyúlási képlete
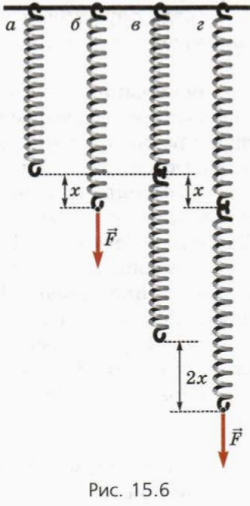
Tekintsük most a második ilyen rugó és csatlakoztassa a rugó, ábrán látható módon 15,6 in. Ebben az esetben azt mondjuk, hogy a rugók sorba vannak kötve.
Találunk merevség kposl rendszer két, sorba kapcsolt rugó.
Amennyiben a nyújtási erő rugó rendszer, az erő az egyes rugó rugalmassági modulusa egyenlő F. A teljes nyúlás a rugó rendszer egyenlő 2x, úgy, hogy minden tavasszal hosszúkás és x (ábra. 15,6 g).
ahol k - a merevség egy rugó.
Így a merevsége a rendszer két azonos sorbakapcsolt rugók 2-szer kisebb, mint a merevségét mindegyik.
Ha sorba van kapcsolva egy másik rugó merevsége, a rugalmas erő a rugók azonos. A teljes nyúlás a rugó rendszer összegével egyenlő a bővítmények a rugók, amelyek mindegyike lehet kiszámítani Hooke-törvény.
8. Bizonyítsuk be, hogy a soros kapcsolás két rugó
1 / kposl = 1 / K1 + 1 / k2. (4)
ahol K1 és K2 - tavaszi merevséget.
9. Mi a a rendszer merevségét a két sorba kapcsolt rugó merevsége 200 N / m és 50 N / m?
Ebben a példában, a a rendszer merevségét a két sorosan kapcsolt rugók kisebb, mint a merevség minden tavasszal. Ez mindig így van?
10. Mutassuk meg, hogy az a rendszer merevségét a két sorba kötött források kevesebb, mint a merevség bármely rugók a rendszer kialakítását.
párhuzamos kapcsolása
Ábra 15.7 ábra a bal párhuzamosan kapcsolt azonos rugók.
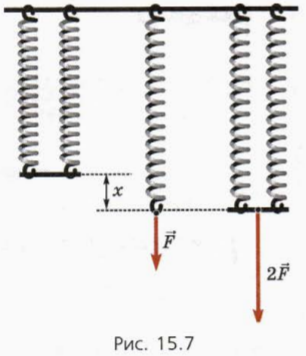
Jelöljük egy rugó merevsége k, és a merevség KPAR tavaszi rendszerben.
11. Mutassuk meg, hogy KPAR = 2k.
Tip. . Ábra 15.7.
Így a merevsége a rendszer két azonos párhuzamos rugó csatlakozik a 2-szer nagyobb merevsége az egyes.
12. Mutassuk meg, hogy közben a párhuzamos kapcsolat a két rugó merevségét K1 és K2
Tip. Párhuzamosan kapcsolt rugók azonos megnyúlása és rugalmas erő a rugó által kifejtett rendszer összegével egyenlő az elasztikus erőket.
13. Két rugóállandója 200 N / m és 50 N / m-párhuzamosan vannak kapcsolva. Mi az a rendszer merevségét két rugó?
14. Igazoljuk, hogy a merevsége rendszer két párhuzamosan kapcsolt rugók nagyobb a rugók merevsége egyes alkotó rendszer.
További kérdések és feladatok
15. ábrázoljuk a modulusa megnyúlás erők a rugóállandó 200 N / m.
16. A kocsi 500 g ráhúzzák a táblázatot egy rugó merevsége 300 N / m, alkalmazása erő vízszintesen. A súrlódás a kerék a kocsi és az asztal lehet figyelmen kívül hagyni. Mi a kiterjesztése a tavasszal, ha a jármű mozog gyorsulással 3 m / s2?
17. A rugóállandó k felfüggesztik súlya m. Mi a nyúlás a tavasz, amikor a terhelés a többi?
18. A rugóállandó k a felére csökkent. Mi a merevség az egyes kialakított rugó?
19. A tavaszi k állandó vágjuk három egyenlő részre, és azokat egymáshoz párhuzamos. Mi a merevség a rugó rendszer alakult?
20. Igazoljuk, hogy az a merevséget és a sorba kapcsolt rugók azonos n-szer kisebb, mint a merevségét egy rugó.
21. megjelenítése, hogy a merevsége az n párhuzamosan kapcsolt azonos rugók n-szer a merevségét egy rugó.
22. Ha két rugó van párhuzamosan kötve, a rugóállandó a rendszer 500 N / m, és ha azonos forrásból sorba kapcsolt, a rugóállandó a rendszer 120 N / m. Mi a merevsége minden tavasszal?
23. Található a sima bár asztal megáll rögzítve a függőleges rugóállandója 100 N / m és 400 N / m (ábra. 15,8). A kiindulási állapotban a rugó nem deformálódott. Melyik lesz egyenlő a cselekvés bár a rugóerő, ha eltoljuk 2 cm-re jobbra? 3 cm-re balra?