A területet a görbe vonalú trapéz az integrál ...
Ma megnézzük, hogyan kell használni a határozott integrál, hogy megtalálják a terület különböző alakzatok síkban egy derékszögű koordináta-rendszerben. Ez a tulajdonság a határozott integrál használják gyakran megoldásában sok ilyen probléma. És elmondom neked a főbb célok ebben a cikkben.
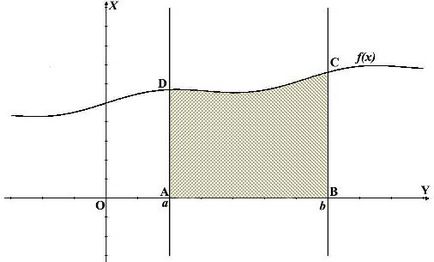
A hajlított trapéz (lásd az első kép) egy szám, amely határolt grafikon egy folytonos, nem-negatív f (x), az [a; b], vonalszakaszok x = a és x = b, továbbá egy szegmensét abszcissza közötti A és B pontok .
Most viszont, hogy a lehetséges kiviteli alakok helyét területen, amely kiszámításához szükséges koordinátarendszerben.
Az első az lenne a legegyszerűbb lehetőség (első szám), a szokásos görbe vonalú trapéz. meghatározásában. Nincs semmi nem kell feltalálni csak hogy az integrál a-ból b az f (x). Mi található a beépített - és tudjuk, hogy a területet a trapéz.
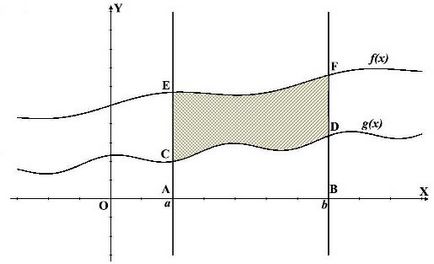
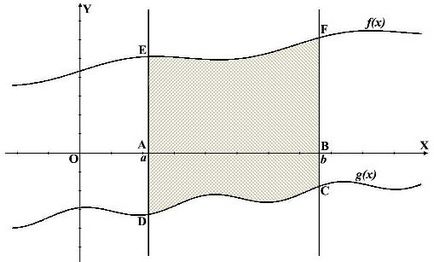
Egy második kiviteli alak, a mi a szám nem korlátozódik az abszcissza tengelyen, és egy másik funkció g (x). Ezért lenne megtalálni a terület CEFD. először is meg kell találni AEFB terület (a szerves f (x)), majd keresse ACDB terület (a beépített g (x)). És CEFD a kívánt területet az ábra. van különbség az első és a második terület a görbe vonalú trapéz. Mivel a határokat integráció ugyanaz, még mindig lehetséges, hogy írjon egy integrál (lásd alább megadott képlet az ábrán), minden attól függ, bonyolítja a funkciót, amely esetben könnyebb lesz megtalálni az integrál.
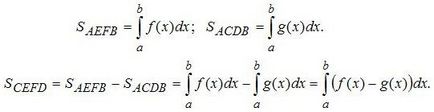
A harmadik nagyon hasonló az elsőhöz, de csak a trapéz elhelyezett nem az x tengely, és ez alatt. Ezért itt kell tennünk az azonos szerves, de egy mínusz jelet, mert az az integrál értékét negatív, és az értéke a terület pozitív lesz. Ha ehelyett a f (x), hogy a függvény -f (x). hogy ő menetrend ugyanaz lesz egyszerűen jelenik szimmetrikusan az x-tengely.
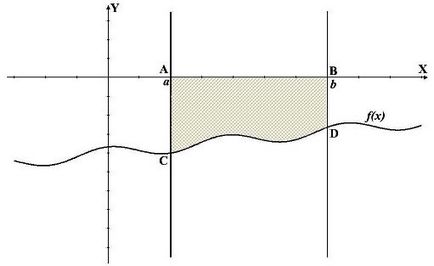
A negyedik lehetőség, mint a mi a szám meghaladja az x tengely, és a program alatt. Ezért először is meg kell találni AEFB területe az ábra. mint az első kiviteli alakban, majd területe az ábra ABCD. mint a harmadik kiviteli, majd tegye őket. Ennek eredményeképpen megkapjuk a szám DEFC területen. Mivel a határokat integráció ugyanaz, még mindig lehetséges, hogy írjon egy integrál (lásd alább megadott képlet az ábrán), minden attól függ, bonyolítja a funkciót, amely esetben könnyebb lesz megtalálni az integrál.
Ez azt tekintik a legegyszerűbb lehetőség, de a gyakorlatban mindig megtalálható a vegyes változata egy pár darab. Konkrét példák a bonyolultabb kombinációja esetén ezeket a lehetőségeket tárgyaljuk a következő cikket.
Kapcsolódó tartalom:
Oszd meg barátaiddal: