meghatározója
Determinánsa a mátrix (a determináns) - négyzetes tömb számok vagy matematikai szimbólumok (δd).
Definíció. A meghatározója a mátrix egy n × n-szám:
ahol (α1 α2 αn ..) - permutációja egész számok 1-től n. N (α1, α2 αn.) - A fordítások számát, a permutáció, az összegezést az összes permutációk a sorrendben várható n.
A meghatározója a mátrix az általánosan jelölt de t (A), | A |. vagy? (A).
Tulajdonságait meghatározó a mátrix.
Tulajdonságai meghatározója - a paraméterek, amelyek a döntés minden algebrai mátrixok.
- A determinánsa az identitás mátrix egyenlő egység, rendre: det (E) = 1.
- A meghatározója a mátrix, ahol két sor (oszlopok) egyenlő, nulla lesz.
- A meghatározója a mátrix, ahol két sor (oszlopok) arányos egymással is nullával egyenlő.
- A meghatározója a mátrixba, amely a sor (oszlop) néhány nullák nulla.
- A meghatározója a mátrixot két vagy több sor (oszlopok) lineárisan függ egymástól is egyenlő nullával csak.
- Ha teszünk egy átültetés, az értéke a meghatározó a mátrix nem változik: det (A) = det (A T)
- A determinánsa a fordított mátrixba. det (A -1) = det (A) -1
- Meghatározója a mátrix ugyanaz lesz akkor is, ha bármilyen a vonal (oszlop), hogy egy újabb sor (oszlop), mielőtt szorozva tetszőleges számú.
- A meghatározója a mátrix nem változik, ha bármelyik sorában (oszlop), hogy adjunk egy lineáris kombinációja más sorok (oszlopok).
- Ha megváltoztatja helyen két sor (oszlop) mátrix determinánsa a mátrix kap egy ellenkező előjelű.
- A közös tényező a sorban (oszlop) könnyen elő az determináns:
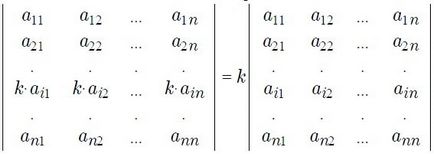
- Megszorozva a négyzetes mátrix n-ed rendű bármely szám nem egyenlő nullával, akkor a meghatározója a mátrix végtermék egyenlő lesz a meghatározó a mátrix eredetileg adott számát mértékben n. B = k · A => det (B) = k n · det (A), ahol a mátrix n × n. k - számot.
- Feltéve, hogy minden egyes eleme minden sorban a meghatározó az összege 2 kifejezések, az eredeti meghatározó összegével egyenlő 2 determinánsok, ahol ahelyett, hogy a helyettesített vonal az első és második szempontjából, illetve, és a fennmaradó vonalak egybeesnek a kezdeti determináns:
- A meghatározója a felső (alsó) háromszög mátrix megegyezik a terméket annak átlós elemek.
- A meghatározója a mátrix termék felel meg a termék ilyen mátrixok determinánsok: det (A · B) = det (A) · det (B).
Keresse meghatározója a mátrix.
Ahhoz, hogy megtalálja a meghatározója a mátrix szükséges ismerni az alapvető tulajdonságait a matricát és a műveletek sorrendjének megoldásánál a mátrixban.
- A mátrixok a rend n = 2 determinánst a következő képlettel: δ = a11 * A22 -a12 * a21
- A mátrixok a rend n = 3 meghatározóak a kofaktorok, vagy az eljárás Sarryusa.
- A mátrix a dimenziójával> 3 bomlik a kofaktorok, amelyek a meghatározó tényezők (kiskorúak). Például, a mátrix determinánsát érdekében 4 számítjuk tágulása sorok vagy oszlopok.
Ahhoz, hogy megtalálja a meghatározó egy mátrix. amely tartalmaz egy mátrix funkcióval, standard technikák alkalmazásával. Például, hogy megtalálják a meghatározója a mátrix a harmadik rend:
Használjuk a terjeszkedés az első sorban:
δ = sin (x) × [cos (x) × 2 - 0 × tg (x)] + 1 × [1 × 0-2 × cos (x)] = 2sin (x) cos (x) - 2cos (X ) = sin (2x) - 2cos (x)
Számítsuk ki a meghatározója a mátrix.
Számítsuk ki a meghatározója a mátrix több módszer, amelyet az alábbiakban felsorolt.
A legnépszerűbb módja annak, hogy kiszámítja a meghatározója a mátrix a kiválasztási módszer a cofactors. Van egy egyszerűbb változata ez a módszer - a számítás a meghatározó segítségével Sarryusa szabályokat. Ezek a módszerek különböznek a számítás a meghatározója egy egyszerű kis mátrix, és ha azt akarjuk számítani a mátrix nagyméretű, akkor is alkalmazhatók, így számítja ki a meghatározója a mátrix:
- a számítás a meghatározója a módszer csökkenti a sorrendben,
- Gauss meghatározó számítási módszer (azáltal, hogy a mátrix a háromszög alak)
- a számítás a meghatározó bomlási módszert.
Az Excel kiszámításához meghatározó funkció használatakor MDETERM = (cellatartományt).