Közvetlen a gépen
Feladat. A pont (2,1), a B (1, -2), C (1,0) a csúcsai az ABC háromszög.
a) Határozzuk meg az egyenlet az ABC háromszög oldalai.
b) Határozza meg az egyenlet egyik felező az ABC háromszög.
c) Mekkora az egyenlet egy ABC háromszög magasságát.
d) Mekkora az egyenlet egyik bisectors az ABC háromszög.
d) Mekkora az ABC háromszög területe.
Az oldatot végezzük egy számológép.
Tekintettel háromszögének koordinátái: A (2,1), a B (1, -2), C (-1,0).
1) koordinátái vektorok
Koordinátái vektorok adja meg:
X = xj - xi; Y = yj - yi
Itt az X, Y koordináták a vektor; xi. yi - a pont koordinátáit, Ai xj. yj - pont koordinátái Aj
Például, a vektor AB
X = x2 - x1; Y = y2 - y1
X = 1-2 = -1; Y = -2-1 = -3
AB (-1; -3)
AC (-3; -1)
BC (-2; 2)
2) A modulok a vektorok
A hossza a vektor egy (X; Y) kifejezve a koordinátái a következő képlettel:
3) közötti szög az egyenes
A közötti szög vektorok a1 (X1, Y1), a2 (X2; Y2) megtalálható a következő képlettel:
ahol a1 a2 = X1 X2 + Y1 Y2
Mi az a szög között az AB és AC
# 947; = ARccOS (0,6) = 53,13 0
4) A vetítés a vektor
A vetítés a b vektor egy vektorba megtalálható a következő képlet segítségével:
Megtaláljuk a vetülete a vektor AB vektor AC
5) háromszög területe
Legyen A1 pont (x1, y1), A2 (x2, y2), A3 (x3; y3) - a háromszög csúcsait, míg a terület általános képlete:
A jobb oldalon az a meghatározó a másodrendű. A háromszög területe mindig pozitív.
Határozat. A kezelés ideje alatt az első csúcs, azt találjuk:
A képlet szerint kapjuk:
6) A szegmens részlege ebben a tekintetben
A sugár vektor r A, osztja a szegmens AB kapcsolatban AA: AB = m1: m2. képlet határozza meg:
A pont koordinátái A adja meg:
háromszög medián egyenlet
Mi felezőpontja BC levél M. Ekkor a pont koordinátáit M találja a képleteket kettéosztott a szegmens.
M (0, -1)
Egyenlet AM medián megtalálják a következő képlet segítségével az egyenlet egy egyenes, amely áthalad a két megadott pont. AM median áthalad pontokon A (2, 1) és M (0, -1), úgy, hogy:
vagy
vagy
y = x -1, vagy y -x + 1 = 0
7) A egyenes egyenlete
Az egyenes vonal áthaladó A1 (x1, y1), és pont A2 (x2, y2), képviseli a egyenletek:
Az egyenes egyenlete AB
vagy
vagy
y = 3x -5 vagy Y -3x +5 = 0
Az egyenes egyenlete AC
vagy
vagy
y = 1/3 x + 1/3 vagy 3y -x - 1 = 0
Az egyenes egyenlete BC
vagy
vagy
y = -x -1 és y + x + 1 = 0
8) Hossza háromszög magassága levonni a pont
A d távolság a pont M1 (x1; y1), hogy a vonal ax + by + C = 0 egyenlő az abszolút érték nagysága:
Azt találjuk, a távolságot a pont (2, 1), és a vonal BC (y + x + 1 = 0)
9) a magassága a vertex egyenlete C
A vonal ponton áthaladó M0 (X0, y0), és merőleges a vonal ax + by + C = 0 van egy irányvektor (A; B), és így által képviselt egyenletek:
Ez az egyenlet megtalálható más módon. Ahhoz, hogy megtalálja ezt a szögletes együttható k1 AB.
Egyenlet AB: y = 3x -5, azaz k1 = 3
Azt találjuk, a lejtőn k a merőleges a feltétele merőlegességének két egyenes vonal: k1 * k = -1.
Behelyettesítve ezt szögletes együttható k1 közvetlen beszerzése.
3k = -1, ahol k = -1/3
Mivel a merőleges áthalad a C pont (1,0), és K = -1 / 3 arra törekszik annak egyenlet formájában: y-y0 = k (x-x0).
Behelyezése x0 = -1, k = -1/3. y0 = 0, azt kapjuk:
y-0 = -1/3 (x - (- 1))
vagy
y = -1/3 X - 1/3
Az egyenlet a felezővonal a háromszög
Azt találjuk, a felezővonal a szög A. A metszéspontja a szögfelező a BC oldalt jelöli M.
Az általunk használt képlet:
Egyenlet AB: y -3x +5 = 0, az egyenlet AC: 3y -x - 1 = 0
^ A ≈ 53 0
Ez osztja ketté a szögfelező következésképpen szög NAK ≈ 26.5 0
A tangense a hajlásszög AB 3 (mert y -3x +5 = 0). A hajlásszög 72
^ NKA≈ 180 0-72 0 108 0 =
^ ANK ≈ 180 0 - (+ 108 0 26,5 0) ≈ 45,5 0
tg (45,5 0) = 1
Szögfelező átnyúlik a pont (2,1), a következő képlet segítségével, van:
y - y0 = k (x - x0)
y - 1 = 1 (x - 2)
vagy
y = x -1
Letöltés: xml
Példa. Vannak csúcsainak koordinátáit az ABC háromszög: A (-3, -1), a B (4; 6) C (8; -2).
Szükséges: 1) kiszámításához a hossza BC oldal; 2) Find az egyenlet a BC oldal; 3) Find a belső háromszög csúcsszöge B; 4) egyenlővé magassága AK levonni az A pont; 5) keresni a homogén koordináták a háromszög súlypontja (a metszéspont felező); 6) Ahhoz, hogy a rajz egy koordináta-rendszert.
- egyenlőségjelet tesznek a súlyvonal a B pont, és kiszámítja a hossza.
- egyenlővé magassága levonni a pont, és kiszámítja a hossza.
- Keresse meg a koszinusza a szög a belső B ABC háromszög.
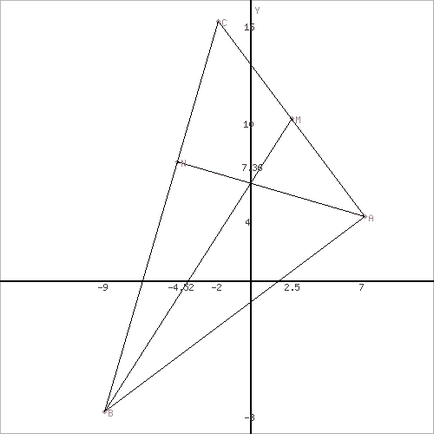
Példa №3. Tekintettel csúcsból (1, 1), B (7, 4), C (4, 5) a háromszög. Keresés: 1) hossza az AB oldal; 2) A belső szög, radiánban 0,001. Tedd rajz.
letöltés
Példa №4. Tekintettel csúcsból (1, 1), B (7, 4), C (4, 5) a háromszög. Find: 1) magassága az egyenlet átszívott a vertex C; 2) a medián egyenlet átszívott a vertex C; 3) A metszéspont a magasságtól háromszög; 4) a hossza a húzott magasság a C csúcs Tedd rajz.
letöltés
Példa №5. Vannak, a háromszög csúcsait ABC: A (-5; 0), B (7; -9), C (11; 13). Adjuk meg: 1) a hossza AB oldal; 2) az egyenlet oldalán AB és AC, és ezek szögletes együtthatók; 3) A terület egy háromszög.
Határozat.
Koordinátái vektorok adja meg:
X = xj - xi; Y = yj - yi
Itt az X, Y koordináták a vektor; xi. yi - a pont koordinátáit, Ai xj. yj - pont koordinátái Aj
Például, a vektor AB
X = x2 - x1; Y = y2 - y1
X = 7 - (- 5) = 12; Y = -9-0 = -9
AB (12; -9), AC (16; 13), BC (4; 22).
A hossza az oldalán a háromszög
A hossza a vektor egy (X; Y) kifejezve a koordinátái a következő képlettel:
háromszög területe
Legyen A1 pont (x1, y1), A2 (x2, y2), A3 (x3; y3) - a háromszög csúcsait, míg a terület általános képlete:
A jobb oldalon az a meghatározó a másodrendű. A háromszög területe mindig pozitív.
Határozat. A kezelés ideje alatt az első csúcs, azt találjuk:
A képlet szerint kapjuk:
Az egyenlet egy egyenes vonal
Az egyenes vonal áthaladó A1 (x1, y1), és pont A2 (x2, y2), képviseli a egyenletek:
Az egyenes egyenlete AB
Canonical egyenes egyenlete:
vagy
vagy
y = -3/4 X -15/4 vagy 4Y + 3x +15 = 0
A meredekség AB egyenes k-val egyenlő = -3/4
Az egyenes egyenlete AC
vagy
vagy
y = 13/16 x + 65/16 vagy 16y -13x - 65 = 0
A meredekség AB egyenes k-val egyenlő = 13/16