nyomás sveta_4

Home | Rólunk | visszacsatolás
Maxwell alapján az elektromágneses mező elmélet jósolta, hogy az eset a felszínen a test elektromágneses hullámterjedés az, hogy nyomást gyakorol rá, amely arányos az energia áramlását hullámok. Ez az érték nagyon kicsi, és mérje meg nagyon pontos eszközök.
Ábra. 17.9. Reakcióvázlat Lebegyev tapasztalat fény által nyomás mérés
1899-ben, orosz kísérleti fizikus Pjotr Lebegyev (1866-1912) végzett kísérletek fényt nyomás mérésére. Reakcióvázlat Lebegyev kísérletet ábrán látható. 17.9. A fényhullám esemény az SPE sen-szerkezet, amelynek fő elemei láb-Kie „szárnyak” 1-4 egyik oldala mindkét szárny úgy megfeketedett, és a másik pedig egy kis tükröt. Structure-szuszpendáljuk 5 a fűtőszál és helyezzük egy üvegedényben, ahonnan a levegő evakuáljuk. A fény egy másik nyomás a megfeketedett és a tükör-nek a szárnyak felületét. Ennek eredményeként, a nyomaték ható a szerkezet, nem nulla. Ugyanakkor az forog. A szál csavart, és ez ad okot, hogy a rugalmas erők, amelyek protivodey-léteznek fény erői nyomás. Amikor a szerkezet, amelyek eltérnek a
kiindulási helyzetbe, nyugalomba került, a pillanatban a rugalmas erők egyenlő a pillanatban a fény erői nyomás. Mivel az idő a rugalmas erő egyenesen arányos a forgásszög design, a forgásszög értékének meghatározásához enyhe nyomást. Az energia, a beeső fény mérése egy hőelem. Mérések azt mutatták, hogy a fény nyomása egyenesen arányos az energia a beeső fény egységnyi idő alatt egységnyi területen a megvilágított felület. Lebegyev rennoe-mérhető fény-nyomás értékét hibáin belül mérések egybeesett által kiszámított érték Maxwell. Tehát Obra zoom Lebedev kísérletileg létét, enyhe nyomás által jósolt Maxwell.
Lebegyev kísérletek egy időben tekinthető az egyik legfontosabb bizonyíték a valós Maxwell létre az elmélet elektromágneses mezőt. Alacsony nyomású is alapján számított ábrázolások fény részecskék sokaságát.
17.6. A nyomás gerenda
Tekintsük az elektromágneses sugárzás, mint a patak fotó új. Egy ütközés a felszínen a foton áthalad a im pulzus. A következménye többszörös ütközések a fotonok felületek Stu nyomást gyakorlunk az elektromágneses sugárzás a felületen.
Legyen egy sík elektromágneses hullám intenzitása I esik egy sík felületen szögben # 952; a normális. A fény reflexiós felület # 961;. Találunk az előre alakos ábrázolások normál által kifejtett nyomás a felület fény. Ebben az esetben, egy sík elektromágneses hullámot kell tekinteni, mint egységes patak foton érkezik a felületen szögben # 952;. Tegyük fel, hogy az összes ilyen fotonok azonos energiával # 949;. A lendület mindegyikük egyenlő lesz
Ahhoz, hogy megtalálja a P nyomás a felület legyen Comput-csatorna, vagy az intézkedés a hatályos F # 9576;. amely hat rá a normális irányban hozzá, majd elosztottuk ezt az erőt a felület S:
A kifejtett erő a felület sugárzás szerint tét átkapcsoló impulzus aránya impulzus lépésekben # 8710; ps, a kapott felületet a fotonok, az idő # 964; amelyekre ez alatti növekmény történt:
növekmény impulzus # 8710; ps felület megegyezik az összeg a hüvelyesek, koto-rozs szerez után számos támadás annak a fotonok. Let p1 - foton impulzus esemény a felszínen, és p2 - visszavert foton impulzus (ábra 17.10.).
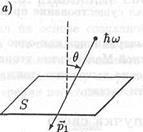
Ábra. 17.11. A törvény lendületmegmaradás egy foton és a felület.
Visszaverődés után felület fogadja psotp foton pulzusát. amely a rá merőleges
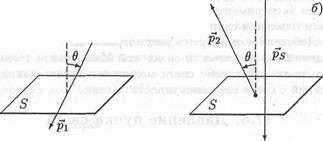
17. ábra. 10. A foton eltalálja a felszíni és visszaverődik
Törvény lendületmegmaradás a rendszer, amely egy foton és a felszíni alábbi egyenlet fejezi ki
ahol PSotr - lendület után gondolkodás felszíni pho-tone. Tegyük fel, hogy a felület tökéletesen sima. Ebben az esetben a mérlegelés fény szöge egyenlő a beesési szög # 952;. Az impulzusok a foton és a felszíni kielégíti a következő egyenletet (17,23) ábrán mutatjuk be. 17.11. Amikor egy foton felszínéről visszaverődő az energia nem változik etsya. Nem is változik a lendület modul: p1 = p2. Ábra. 17.11 könnyű megtalálni a nagysága pSomp
Ha az eset foton impulzus p1 irányul szögben # 952; a normális, a reflexió után felület fogadja foton lendülete
Ha a foton elnyelődik a felület, a törvény lendületmegmaradás lesz a forma
azaz felület fogadja az impulzus p1 elnyelt foton. A vetítés a kapott impulzus a felületre merőleges ez lesz
Let alatt # 964; a felületen a csepp N fotonok. Energia sugárzás Wnad alá, ez idő alatt a felület megegyezik a termelés-irányítási jogkör # 949; egy foton a szám:
Ugyanígy csatlakozik Womp energiájú sugárzás tükröződik a felület, ez idő alatt, és a fotonok száma tükrözi Nomp:
reflexiós együttható # 963; Womp az aránya az energia a visszavert sugárzás a felületi energia Wnad sugárzást is:
Helyettesítő ebben az egyenletben a (17.27) és (17.28). megkapjuk
Mivel a több elnyelt felszíni
Eljutunk a képlet
alatt # 964; felület szerez egy lendület
Nyert a felszíni fotonok időbeli # 964;, amelyre ez a növekmény történt:
A definíció Wnag sugárzási energia felületére eső idővel # 964;, a termék az I intenzitását a sugárzás a területen S cos # 952; keresztmetszetének egy fénynyalábot és egy időben # 964;:
Használata (17.27), azt látjuk, a fotonok számát incidens felületén egy időben # 964;:
Behelyettesítve ezt a kifejezést a (17,32). megkapjuk
Végül, képletek (17.21) és (17.22) vezet a következő kifejezés a kifejtett nyomás a sík felületre a fény-hullám a beeső rajta szögben # 952;:
Ha a felület egy tükör, és tükrözi azt padayushee sugárzást (# 963; = 1), egyenletet (17,34) ad egy értéket
Ha a felület az abszolút fekete elnyeli az összes eset-yuschee neki sugárzás, a reflexiós együttható # 963; = 0 és a sugárzási nyomás a felszínen lesz
Így a sugárzási nyomás a tükör felületén kiderül,-JELÖLI kétszer nagyobb, mint a fekete.
17.7. Nyomás izotrop sugárzást *
Találunk a nyomást gyakorolt egy lapos sugárzás izotróp-kuyu felületre. Hagyja, hogy a sugárzási energia sűrűsége w. Úgy véljük sugárzás izotrop, mint egy gyűjtemény lapos elektromágneses hullámok szaporító minden lehetséges irányban tér-gödrök. Isolate a „szűk keresztmetszet” a kúp részét hullám terjedési irányát, amely abban rejlik ezen belül kúp (ábra. 16,4). Ha a térszög d # 937; kúp elég kicsi, akkor a kiválasztott hullám és így csaknem síkhullám intenzitás-dI, amely hozzájárul ahhoz, hogy olyan (1.20), arányos a energiasűrűség dw:
A energiasűrűség arányos a kiosztott hullámok térszög:
Ezek az arányok vezetnek képletű (16.21)
ahol szerint (16,24)
A kifejtett nyomás a felszínen a kiválasztott sugárzás megtalálják a általános képletű (17,34), helyette az intenzitása I dI:
Behelyettesítve expresszió (17.37) átalakítja ezt a képletet formájában
Mert sugárzást bármilyen felületen a fél - CIÓ, szög # 966; Ez változik 0 és 2π, és az a szög # 952; - 0 és n / 2. Így, a sugárzás izotrop nyomás egyenlő a kettős integrál
kiszámítása, amely vezet a képlet
A fűtött test nem csak tükrözik, és elnyelik az elektromágneses sugárzás, hanem a kibocsátó saját. Által kibocsátott sugárzás a test úgy, nyomást fejt ki a felületén. Amikor egy egyensúly a test és a sugárzás bármely részét a testfelület a félig térben megy sugárzás amelynek energiája az energia betétek sugárzást a fele a rész. A összege nyomások a visszavert, elnyelt és kibocsátott sugárzás a test nem függ a tulajdonságait a testfelület. Így, figyelembe véve a sugárzási nyomás egyensúlyi nyomás a kibocsátott sugárzás a test által megtalálható a következő képlettel (17,38), üzembe az abban # 963; = 1. Ennek eredményeként azt látjuk, hogy az egyensúlyi sugárzási nyomás társul az energia sűrűség arányú