S komplex számok
A divízió határozzuk meg az inverz szorzás. Egyedi két komplex szám Z1 és Z2 ≠ 0 komplex szám Z, amely, ha szorozva Z2. Ez adja meg a számot z1. t. e. z1 / z2 = z, ha Z2 Z = Z1.
Megoldása a rendszer, azt látjuk, az értékeket az x és y:
A gyakorlatban ez az arány két komplex szám megtalálható megszorozzuk a számláló és a nevező száma kettős nevező ( „megszabadulni a képzeletbeli nevező”).
P.2.5.Izvlechenie gyökerek komplex számok kivonat gyökér n-ed-fokú definiáljuk inverz építése egy természetes erő.
Kornemn-edik hatványa a komplex szám Z egy komplex szám ω, kielégíti a következő egyenletet ω n = z, t. E., Ha ω n = z.
Ha tesszük z = r (cosφ + isinφ), és ω = r (cosθ + isinθ), akkor definíció a gyökér és a képlet Moivre kapjunk
Z = ωn = rn (cos nθ + ISIN nθ) -r (cosφ + isinφ).
Így van egy r n = r, nθ = φ + 2πk, k = 0, -1,1, -2,2. Ahhoz, hogy
és (számtani gyökér).
Ezért ravenstvoprinimaet megtekintés
Kapunk értékei n különböző gyökerek. Más k értékeket, mivel a periodicitás a koszinusz és szinusz, megkapja az értékét a gyökér, amelyek azonosak a már megtalált. Tehát van k = n
Így minden olyan z ≠ 0 gyökere n-edik hatványa a száma Z pontosan n különböző értékeket.
Record komplex számok Z1 = -1 + i és Z2 = -1V trigonometrikus és exponenciális formák.
Megoldás: Ahhoz, hogy z1
t. e. J = o. Ezért -1 = cosπ + isinπ = E iπ.
Megoldás: Írunk az első szám trigonometrikus alakban:
A képlet szerint, van Moivre
A trigonometrikus forma egy komplex szám osztódó képlet
Amikor elosztjuk komplex számok egységek, illetve vannak osztva, és érvek, illetve kivontuk.
Megoldás: a) Mi írjuk a radikális kifejezést a trigonometrikus alakban:
.
b) Re-levelet a radikális kifejezést a trigonometrikus alakban:
-1 = Cosπ + isinπ.
Amikor k = 0 megkapjuk ω0 = cos / 2 + isin / 2 = i, és szerezzen k = 1
Határozat. Műveleteket végeznek, mint a polinomok
Építsd a komplex síkon és képviselt trigonometrikus és exponenciális formáját az alábbi komplex számok:
1) 2) 3) 4) 5).
Határozat. Először építünk ezeket a pontokat a komplex síkban
Most képzeld el őket a trigonometrikus és exponenciális formában:
Mivel a második negyedévben 2-, majd
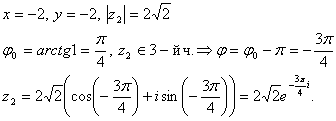
Képviseli az exponenciális formában:
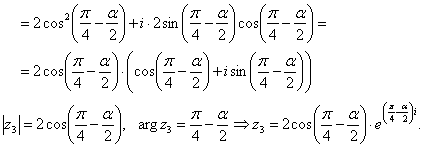
1) képviseli a szám formájában trigonometrikus
A képlet szerint Moivre get:
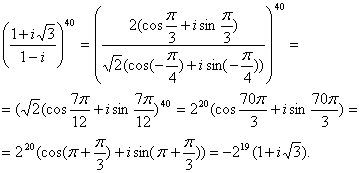
Szerkesszünk egy grafikont a funkciót.
Ez a funkció a formában. azaz egy még funkciót, és így a grafikon szimmetrikus tengelyéhez képest OY.
Tekintettel arra, hogy. meg kell felhívni a grafikon funkciók Tologatva OX tengelye a grafikon 4 egység.
1) azt plot funkció (ábra11);
2) eltolva azt 4 egység OX tengelye a grafikon a konstrukció (ábra 11b) .;
3) fenntartjuk a jobb oldalon (a) a funkció és a kijelzőn a generált szimmetrikusan OY tengelyre. Annak tisztázása meghatározott ütemezés ütemtervét a metszéspont a tengely OY. Amikor. azaz generált metszéspontja tengely OY (0, -2). Menetrend funkció megjelenik fig.11c.
Szerkesszünk egy grafikont a funkciót.
Mivel ez egy páros függvény és grafikon szimmetrikus tengely OY. X értéke. amelyben a kifejezés alatt logaritmus jele eltűnik, nem érvényes az x és egyúttal segítenek megtalálni a függőleges asymptote. Megtalálni őket.
.
A grafikon négy függőleges aszimptotákkal
.
Mi határozza meg nulla. Van:
.
Tehát a tengelyen OX, van öt pont a függvény grafikonján:
(-2, 0), (-1, 0), (0, 0), (1, 0), (2, 0). Ütemezés funkció négy asymptote. A telek meg kell tudni, hogy melyik oldalon a gráf ágakat közelebb a aszimptotákkal. Ez elegendő ahhoz, hogy meghatározzuk a időközönként állandó jel funkció. Emlékezzünk vissza, hogy
.
Tehát, ha. akkor Y> 0, és ezért, ha. akkor. Ezért, a grafikon a függvény a tartományban