Pitagorasz-tétel
Visszatérve a téglalap kezdtük vizsgálni az előző cikkben. Mi érdekli az arány a oldalainak hossza a téglalap és a hossza az átlós. Vagyis, mi oldja meg ugyanazt a problémát, és hogy
Mégis évszázadokon napjainkig egyiptomiak a gyakorlati tapasztalatok alapján megállapítottuk, hogy ha az egyik oldalon a derékszögű háromszög egyenlő 3 egység, és a többi - 4 db, a hossza a átfogója 5 egység. Ebben az esetben, az arány az átfogó és az egyik oldalon egyenlő $ \ frac54 $ a hosszabb oldalon, és 5 $ \ frac53 $ rövidebb.
A görögök jött a probléma általánosabb értelemben. Meg kell találni a minta, ez az arány az oldalainak hossza a téglalap és a hossza az átló minden derékszögű háromszög.
Ahogy a történet halad, a nagy görög matematikus Pythagoras felfedezett egy mintát. Úgy találtuk, hogy minden derékszögű háromszög a következő feltételek teljesülnek:
A négyzetének összege egyenlő az oldalak a tér a átfogója.
Ez az állítás már az úgynevezett Pitagorasz-tétel. Tétel még mindig viseli a nevét a nagy görög, bár most már tudjuk, hogy még a 600 évvel korábban Püthagorasz, az ókori kínai már tudta ezt a kapcsolatot.
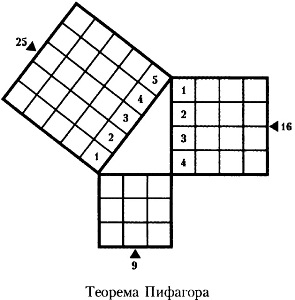
Ellenőrizzük a tétel oldalú háromszög a 3. és 4. A tér egyik oldalán 3 × 3 = 9, négyzet másik oldalon 4x4 = 16. A négyzetösszegek: 9 + 16 = 25, azaz a tér a átfogója egyenlő 25, ezért a átfogója egyenlő 5.
Vegyünk egy másik háromszög oldala, 5 és 12.
Ehhez az arány a átfogója a háromszög egyenlő az oldalon a $ \ frac $ a rövid oldalon, és $ \ frac $ a hosszú oldalon.
A Pitagorasz-tétel. Megtalálható az arány az átfogó, és mindkét fél minden derékszögű háromszög. Görög matematika lélegezni könnyű, a probléma megoldódott. A legfontosabb dolog az volt, hogy tétel érvényes minden derékszögű háromszög, beleértve természetesen, és egyenlő oldalú, amely a derékszögű háromszög, amelyben mindkét fél egyenlő. De mi most érdekel pontosan ilyen háromszög.
Egyikük az ábrán a bal oldali
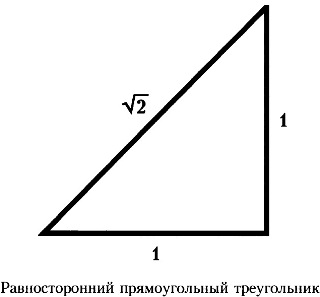
Egyszerűbb a feladat, és feltételezik, hogy az oldalán a háromszög egyenlő 1. Ekkor a tér oldalán egyenlő 1x1, és a négyzetének összege a fél egyenlő 1x1 + 1x1 = 2. Szerint a Pitagorasz-tétel, a tér a átfogója értéke 2, és az átfogó egyenlő, illetve $ \ sqrt $.
Kapcsolódó tartalom:
Oszd meg barátaiddal: