Példák integrációja racionális függvények (frakciók)
Itt az integrál jel érdemes racionális függvény, mivel az integrandus egy töredéke a polinomok. A mértéke a nevező a (3) kisebb, mint a foka számláló polinom (4). Ezért először ki kell választania egész részét a frakció.
1. Jelölje egész részét a frakció. Osszuk x 4 x 3 - 6 x 2 x 11 + - 6.
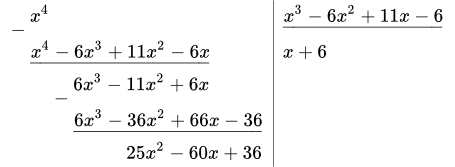
itt
.
2. Helyezzük a nevező faktorizációt. Ehhez meg kell oldani a harmadfokú egyenlet:
.
Tegyük fel, hogy van legalább egy egész root. Akkor ez egy osztója 6 (a kifejezés nélkül x). Ez az egész gyökér lehet az egyik szám:
1, 2, 3, 6, -1, -2, -3, -6.
Behelyettesítve x = 1.
.
Tehát, találtunk egy gyökér x = 1. osztani x - 1.
itt
.
Megoldjuk a másodfokú egyenletek.
.
A gyökerek az egyenlet.
majd
.
3. bomlanak részleges frakciók.
Tehát, találtunk:
.
Mi integrálja.
Itt a számláló - a polinom foka nulla (1 = x 0). A nevező - a polinom harmadik foka. mivel 0 <3. то дробь правильная. Разложим ее на простейшие дроби.
1. Tegyük bővíteni a nevező faktorizációt. Ehhez meg kell oldani az egyenletet a harmadik fokozat:
.
Tegyük fel, hogy van legalább egy egész root. Akkor ez egy osztója 3 (a kifejezés nélkül x). Ez az egész gyökér lehet az egyik szám:
1, 3, -1, -3.
Behelyettesítve x = 1.
.
Tehát, találtunk egy gyökér x = 1. Osszuk x 3 + x 2 - 3 x - 1.
Mi megoldjuk a másodfokú egyenlet:
x 2 + x + 3 = 0.
Find a diszkrimináns: D = 2-4 január · 3 = -11. mivel D <0. то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
2. Mi bomlanak részleges frakciók. Keresünk terjeszkedés formájában:
.
Felszabadult a nevező megszorozzuk (x - 1) (x 2 + x + 3).
(2.1).
Mi helyettesíti x = 1. Ekkor x - 1 = 0.
.
Behelyettesítve a (2.1) x = 0.
1 3 = A - C;
.
Egyenlővé a (2.1) az együtthatók az x 2.
;
0 = A + B;
.
Tehát megtaláltuk a bővülés részleges frakciói:
.
3. integrálása.
(2.2).
Kiszámító második integrál izolátum a számláló és a nevező a származék, így a nevező négyzetösszeg.
.
Mivel az x 2 + x + 3 = 0 nincs valódi gyökerei, x 2 + x + 3> 0. Ezért, a jel modul elhagyható.
Itt az integrál jel érdemes egy töredéke polinomok. Ezért az integrandus egy racionális függvény. A mértéke a számláló értéke 3. A mértéke a nevező 4. Mivel 3 <4. то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
1. Tegyük bővíteni a nevező faktorizációt. Ehhez meg kell oldani az egyenletet a negyedik fokozat:
.
Tegyük fel, hogy van legalább egy egész root. Akkor ez egy osztója 2 (a kifejezés nélkül x). Ez az egész gyökér lehet az egyik szám:
1, 2, -1, -2.
Behelyettesítve x = -1.
.
Tehát, találtunk egy gyökér x = -1. Osszuk X - (-1) = x + 1.

Így
.
Most arra van szükség, hogy az egyenlet megoldásához a harmadik fokozat:
.
Feltételezve, hogy ez az egyenlet egy gyökér, ez a tényező a 2 (a kifejezés nélkül x). Ez az egész gyökér lehet az egyik szám:
1, 2, -1, -2.
Behelyettesítve x = -1.
.
Így találtunk egy másik gyökere x = -1. Lehetséges lenne, mint az előző esetben, osztani polinom. de mi a csoport tagjai:
.
Mivel az x 2 + 2 = 0 nincs valódi gyökerei, kaptunk bővülése a nevező a tényezők:
.
2. Mi bomlanak részleges frakciók. Keresünk terjeszkedés formájában:
.
Felszabadult a nevező megszorozzuk a (x + 1) 2 (x 2 + 2).
(3.1).
Behelyettesítve x = -1. Ezután x + 1 = 0.
.
Behelyettesítve X = -1, és emlékeztet arra, hogy x + 1 = 0.
;
;.
Behelyettesítve a (3.1) x = 0.
0 2 = 2 A + B + D;
.
Egyenlővé a (3.1) az együtthatók az x 3.
;
1 = B + C;
.
Tehát megtaláltuk a bővülés részleges frakciói:
.