kettős konverziós
A fő tulajdonsága a projektív sík - „szimmetria” szerepek pontok és vonalak a definíciókat és tételeket, és kettősség hivatalossá a koncepció. Két módja van, hogy ez a kettősség: az egyik, hogy a nyelvet használja (lásd: „kettősség” elv alább.), A másik, egy sokkal funkcionális megközelítés. Ezek teljesen egyenértékű, és mindkét szolgálnak a kiindulási pont változatai axiomatikus geometria. A funkcionális megközelítés van összefüggés a geometria, amely az úgynevezett kettősség. A konkrét példák ilyen leveleket építhető sokféleképpen. sík kettősség koncepció könnyen kiterjeszthető bármely véges duális projektív geometria.
Ha meghatározzuk a projektív sík beesési axiomatically szerkezetét tekintve ponthalmaz P. sor vonalak L és bináris reláció előfordulása I. meghatározza, hogy mely ponton át egyenes vonalak, amelyek lehetséges, hogy határozza meg a kettős síkon szerkezetét.
Ha kicserélt szerepek „pont” és „egyenes” a szerkezet előfordulása
Kapjuk kettős szerkezete
ahol I * - inverz kapcsolat [en], hogy I. C * is projektív sík, az úgynevezett kettős (dual) a sík C.
Ha a C és C * izomorf, akkor C nevezzük önduális. Projektív PG síkban (2, k) minden mező (vagy, általánosabban, bármely gyűrűs részlege izomorf kettős) K önduális. Különösen véges rendű síkon Desarguesian mindig önduális. Azonban, többek között a nem-Desarguesian síkok [en] * léteznek önduális (például Hughes sík [en]), nem önduális (például, a Hall-sík).
A projektív sík nyilatkozatot pontot, repülőgépek és azok előfordulási nyert másik ilyen jóváhagyást cseréje a „pont” és „vonal” (a változás, ha szükséges, nyelvtan) az úgynevezett duális állítás. Kettős beszámoló „Két pont áthalad egy egyedi tétel” lesz „Két vonalak metszik egymást egy pontban.” A formáció a kettős jóváhagyására nevű dualization jóváhagyásra.
Ha az állítás igaz egy projektív sík C, akkor a kettős állítás igaznak kell lennie a kettős C * síkra. Ez abból következik, hogy a dualization minden utasítást a bizonyítás „C” járul hozzá az igazolást „C *”.
A dualitás elve sík mondja dualization bármely önduális tételeket projektív síkon C létrehoz egy másik bizonyos tétel a C.
Ez a koncepció lehet általánosítani kettős háromdimenziós térben, ahol a „pont” és a „sík” változtatni a szerepeket (és a vonalak egyenesek maradnak). [1] Alapelv Ez vezet helyet kettősség. Lehetséges további általánosítás (lásd alább).
Ezek az elvek egy jó ok a használata „szimmetrikus” kifejezés az aránya előfordulása. Tehát ahelyett, hogy kínál „pont rajta van az egyenesen” akkor lehet mondani, „pontot és közvetlen esemény”, és a jóváhagyási dualization elég szó a pont és a vonal a váltási ( „egyenes vonal és egy pont esemény”).
A definíció szerint a projektív sík egy sor pontok és vonalak, és a projektív transzformáció képes megjeleníteni pontot a pontok és vonalak egyenesek. Egy ilyen átalakulás nevezzük kollineáció. [2] Figyelembe véve a projektív sík kettősség tartják egy másik térképet, amely rámutat a egyenes vonalak, és a vonalak - pont. Egy ilyen térképet nevezzük korreláció. [3] A vetített kijelző követelményei határozzák meg megőrzése
1) az előfordulási pontok és vonalak 2) kettős arány [4]
A második követelmény használ harmonikus négyszeres pont egy egyenesen, egy sor pontok kialakítására projektív [en]. fogalmának kétsugaras irányítsa [en] pontnál.
dual tételek
Mivel a valós projektív sík PG (2, R) jelentése önduális, számos jól ismert kijelentések, amelyek kettős egymáshoz. Köztük:
Kettősség térképen
Dualitás (sík) - leképezzük az projektív sík C = (P, L, I) között kettős C * = (L, P, I *), megőrizve az ingatlan beesési. Így a kettősség (sík) σ olyan pontot képvisel az közvetlen és egyenes a pont (P σ = L és L σ = P), oly módon, hogy ha Q fekszik a vonalon m (jelöljük QI m), akkor Q σ I * m σ ⇔ m σ σ IQ. A kettősség (sík) egy izomorfizmus úgynevezett összefüggés. [5] Az megléte korrelációs eszköz selfdual projektív sík.
Abban a speciális esetben, ha a projektív sík típusú PG (2, K), ahol K - ferdetest, az úgynevezett kölcsönös kettősség átalakulás. [6] szerint az alapvető tétel a projektív geometria [en] egymásba a készítmény a automorphic funkciója K és projektív transzformáció. Ha a automor az identitás, a kölcsönös átalakulás az úgynevezett projektív korreláció.
Korreláció a másodrendű (involúció) nevezzük polaritású. Ha a korreláció nem a polaritást, akkor φ 2 nem triviális kollineáció.
Ez a kijelző koncepció lehet terjeszteni magasabb dimenziók a tér, úgy, hogy a referencia-sík lehet távolítani.
A kettőssége magasabb dimenziók
A dualitás projektív sík egy speciális esete a dualitás projektív terek. Konverziók PG (n, k) (amelyek jelöljük KP n), ahol K - mező, cseréje R dimenzió objektumokat a tárgyak a dimenzió n - 1 - R (= kodimenziós r + 1). Így egy projektív térben n dimenziós a pont (dimenzió 0) fog megfelelni hipersíkokat (kodimenziós 1), a vonalak áthaladó két pont (dimenzió 1) felel meg a kereszteződés két hipersíkokat (kodimenziós 2), és így tovább.
Point of PG (n, k) lehet tekinteni, mint egy nem-nulla vektor a (n + 1) dimenziós vektortér feletti K., amelyben azonosítjuk a két vektor, ha eltérnek csak skaláris szorzás. Egy másik módja a bemutató pontok n-dimenziós projektív tér - mind egyenes vonalak az origón áthaladó Kn + 1. amely az 1-dimenziós vektort altér. Így, n dimenziós vektort mezők altér Kn + 1 (n - 1) dimenziós hipersíkot geometriai projektív n terek felett K.
Egy nem nulla vektor u = (. U0, U1 un) Kn + 1, hogy meghatározza (n - 1) - dimenziós geometriai altér (hipersíkot) Hu,
u vektor. használunk, hogy meghatározza a hipersík, jelöli uH. és terjeszti a megfelelő pontban a végén a vektor, használjuk a jelölést uP. Ami a szokásos skalárszorzat. Hu = xP. uH • xP = 0> gombot. Mivel a K egy mező, a skalár szorzat szimmetrikus, ami azt jelenti, uH • xP = u0 x0 + U1 x1 +. + Un xn = x0 u0 + x1 U1 +. + Xn un = XH • felfelé. Megadhatja a kölcsönös közötti átváltás a felfelé ↔ Hu pontot és hipersíkokat. Ez az összefüggés lehet terjeszteni a közvetlen kialakított két pontot, és a kereszteződés két hipersíkokat, és így tovább.
A projektív sík PG (2, K), amely a területen K van megfelelő: homogén koordináták (a, b, c) ↔ vonalak által adott egyenletek ax + by + cz = 0. A projektív térben PG (3, K) megfelelő külleme pont homogén koordinátákkal (a, b, c, d) ↔ sík által adott egyenletek ax + by + cz + DW = 0. Ez a levelezés is mutatja, a által meghatározott egyenes két pont (a1, b1, c1, d1) és (a2, B2, C2, D2), egy egyenes vonal, amely a két síkja egymást metszi egyenletek által meghatározott a1 x + b1 y + c1 z + d1 w = 0, és A2 x + b2 y + c2 z + d2 w = 0.
A poláris leképezések valós projektív 3-dimenziós térben PG (3, R) pontok megfelelnek a repülőgépek és a tételek megfelelnek a sorokat. A szilárd geometria tartja a kettős poliéder. ha a pontok kettős arcok és élek kettős élek, úgyhogy kettős ikozaéder, dodekaéder. és a kocka kettős oktaéder.
Geometriai építése kölcsönös átalakulás
Érték PG (2, R) homogén koordinátákkal írhatjuk le geometriailag. Erre a célra az igazi modell projektív sík [en] „egység gömb azonosító antipodes [7]”, vagy azzal egyenértékű, a modell vonalak és síkok, az origón áthaladó, a koordinátarendszerben R 3. társítani a sor, az origón áthaladó, síkjára merőleges a talp, az origót tartalmazó. Ha ezt a modellt tartják egyenes pontok és a sík - egyenes projektív sík PG (2, R), ez az összehasonlítás válik levelezés (és tulajdonképpen - poláris mapping) A projektív sík. Gömb alakú modell lehet beszerezni, mint a kereszteződésekben a vonalak és síkok az origón áthaladó az egység gömb központ a származási. Közvetlen metszi a gömböt két átellenes pontokat, amelyek azonosítják, így egy pontot a projektív sík, a gép a kereszt köre nagy körökben. amelyek közvetlen projektív sík.
Az a tény, hogy egy ilyen összehasonlítás „megmenti” az előfordulási, könnyű megmutatni a modell vonalak és síkok. Point incidens egy sort a projektív sík az egyenes síkjában fekvő a modellben. Szerint az összehasonlítás, a sík válik áthaladó egyenes vonal a származási és merőleges a síkra. Ez a kép (egyenes vonal) merőleges bármely egyenes síkjában fekvő, különösen, és az eredeti vonal (a pont a projektív sík). Minden egyenes vonalak a referenciasíkra merőleges vonal, amely egy síkot, amely a sík a kapcsolódó forrás vonalat. Így a közvetlen kép rejlik a képsík, hogy az előfordulási gyakorisága megmarad.
Lengyelek és Polars
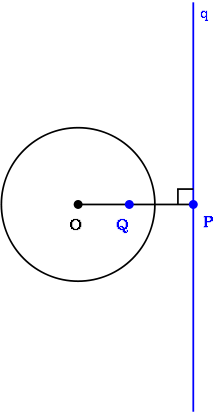
A pólus és poláros kerülete O. P = Q”. q - poláris számára Q. Q - pole q.
Az euklideszi térben, rögzítjük a C kör O középpontú r sugarú. Minden pont kivételével P. O. meghatározza a kép Q”. így OP • OQ = R 2 megjelenítve P → Q úgynevezett inverziós [en] [8] képest a kör C. Közvetlen q. P. merőlegesen áthaladó OP. Ez az úgynevezett a poláris Q pont tekintetében a kerülete C.
Legyen q - egy vonal nem halad át O. csepp egy merőleges O q. amely metszi pontban q P (O van a legközelebb a vonal pontjában q). A kép Q pont (P pont), amikor inverzió nevezzük pólus C vonal q. Ha a pont fekszik egy egyenes vonal M Q (amely nem halad át O), a pólus vonal q fekszik a poláris M pont, és fordítva. A folyamat megőrzi a beesési, amely pontok és vonalak bejut a Polars és pólusok, tekintetében a C az úgynevezett projektív transzformáció. [9]
Ahhoz, hogy ez a folyamat a kölcsönös átalakulás euklideszi térben (nem projektív sík) ki kell terjednie a kiterjesztett euklideszi síkban úgy, hogy a vonal a végtelenben [en] és pont a végtelenben [en]. amelyek ellen egyenest végtelenig. Ez a kiterjesztett sík, definiáljuk a poláros O pont, mint egy vonal a végtelenben (és O a pole a végtelenben), és a pólusok egyenes vonalak áthaladó O végtelenben ponton, ahol, ha a vonal meredeksége s (≠ 0), a pólus végtelenig megfelelő pontban az osztály a párhuzamos vonalak -1 / s lejtőn. Pole az x-tengely - ez az a pont, végtelen függőleges vonalak és a pole y tengelyen - az a pont a végtelenben vízszintes vonalak.
Építőipari polár transzformáció inverzió kört a fenti lehet összefoglalni segítségével inverzió kúpszeletek (a síkban kiterjesztett valós). Kölcsönös konverzió, így előállított, egy másodrendű projektív korreláció, azaz poláros átalakulás.
Feltérképezése a gömb a síkra
projektív sík modell a készülék gömb izomorf (figyelembe véve az előfordulási tulajdon) sík modell, ahol a sík projektív vonal kiterjesztették a végtelenségig. Ebben a modellben az ellenkezője pont a gömb (középpontjához képest), akkor egy pont.
Leképezi a pontokat a gömb pont a síkon, azt feltételezzük, hogy a gömb érinti a sík egy bizonyos ponton, és ezt a pontot vesszük a származási gépet. Most felhívni a sort a pont a gömb és az a gömb középpontján. Ez a vonal keresztezi a gömb egy bizonyos ponton. A kapott pont használható, hogy össze egy egy-az-egy leképezés
Egyenes síkbeli modellek előrejelzései nagy köröket gömbök közvetlen a gépen, és az elején a 3-dimenziós koordinátákat lehet sík, és ez metszi a gömböt egy nagy kört.
Mint látható, bárki lehet, mint egy nagy gömb kör projektív pont megfelel egy merőleges arra a síkra, amely a kör abban rejlik, és amely lehet leírni, mint ambivalens. Ez a vonal metszi a érintősík, és ez azt mutatja, hogy hogyan térkép egy ponton a gépen minden sora ezen a síkon úgy, hogy a pont a kettős vonal.