Távolság meghatározására egy pont síkra geometria, matematika

A távolság a pont a sík megegyezik a hossza a merőleges egy pont a sík és ábrázoló geometria grafikusan szerint határozzuk meg a következő algoritmus.

1. A sík alakítjuk egy kinyúló helyzetben merőleges vetülete transzformációs eljárások.
2. A pont a sík merőleges csökken, és megtalálja a megfelelő hosszúságú. Az irány merőleges vetülete alapján van meghatározva a tétel a kiálló derékszögben.

Tekintsük hogyan hajtsák végre az algoritmus által létrehozott minket a gyakorlatban. Az alábbi ábra grafikus ábrázolás szükséges, hogy meghatározzuk a távolságot a pont az N és a sík α, egy előre meghatározott ABC háromszög.

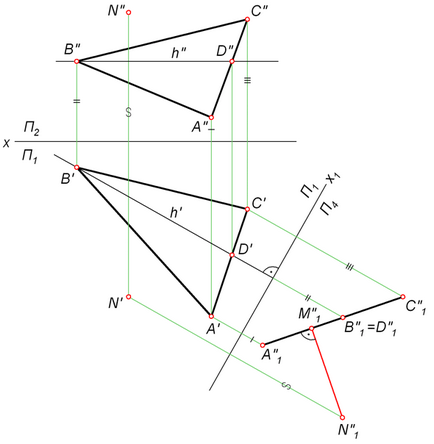
• Tetején keresztül B „” A''B''C háromszög „” tartsa a nyúlvány H „” vízszintes h. Kommunikációs vonalak találni h”.
• Fordítás ABC kiálló helyzetbe. Ehhez h merőleges bevezetni egy új frontális síkban P4. Mi vetíteni ezt a pontot N és az ABC háromszög.
• Pontból N''1 tölteni N''1 M''1 ⊥ A''1 C''1. szegmenshossz N''1 M''1 - a szükséges távolságot a síkja az ABC háromszög, és a pontot N.

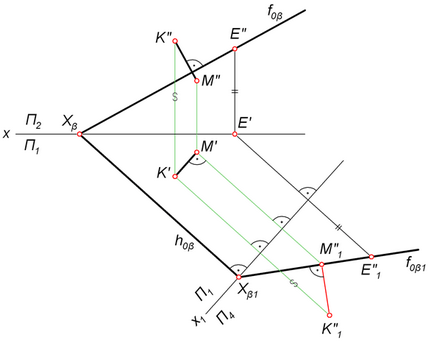
Meghatározásához szükséges értéke közötti távolság K pontot és egy síkban β, egy előre meghatározott nyomait. Ezzel szemben az előző probléma nincs szükség, hogy tartsa a vonalat szinten, hiszen a szerepet a vetítés h0β.

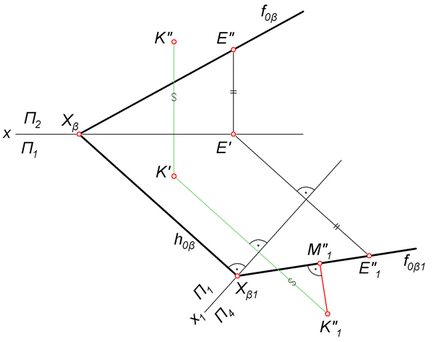
• Β lefordítani síkban kiálló helyzetbe. Ebből a célból, amely merőleges a pálya h0β bevezetni további frontális síkban P4. A közvetlen f0β egy tetszőleges távolságra E, a mi határozza meg a vetítés E ', E „és E''1. Keresztül E''1 és X0α1 magatartás közvetlen f0β1. ezt követi a gépen β P4. A közlemény szerint vonal határozza meg a vetítés K''1 pont K.
• K''1 a merőleges K''1 M''1 felé közvetlen f0β1. szegmenshossz K''1 M''1 - értékét a kívánt távolság K a p.

Ha szeretné, hogy a szegmens a vonatkoztatási sík KM rendszer, ez történik inverz transzformáció, amint azt az alábbi ábra.