Heteroszkedaszticitását grafika econometrics

A találmány egyik előfeltétele a MNC kell diszperzióját a maradékok volt homoskedastic. Ez azt jelenti, hogy minden egyes tényező értéke X maradékok e azonos szórás. Ha ez a feltétel nem teljesül, akkor van heteroszkedaszticitást. A jelenléte heteroszkedaszticitás lehet bemutatni a korrelációs mezőben (lásd. Ábra.).

Homoszkedaszticitás maradványok azt jelenti, hogy a variancia a maradékok jelentése azonos az egyes X értéke a háromdimenziós kép, ez lehetséges a következő grafikonok, hogy illusztrálják a homo- és heteroszkedaszticitás

Ábra a homoszkedaszticitás azt mutatja, hogy minden egyes X értéke, a szermaradvány eloszlását az egyformán eltérően heteroszkedaszticitás.

A többszörös regressziós stílusok a leglátványosabb módon tanul homo- és heteroszkedaszticitást.

A jelenléte heteroszkedaszticitás alkalmazása bizonyos esetekben vezet torzított becslések a regressziós együtthatók, bár a torzítatlan becsléseinek a regressziós együtthatók, mint általában, feltéve, hogy megfelel a második MNC háttérben, t. E. maradékai függetlenséget és az érték tényezőket. Heteroszkedaszticitásra lesz hatással hatékonyságát csökkentő értékelések b. A cha stnosti, rendkívül nehéz használni a képlet a standard hibája regressziós együttható Sb, amely feltételezi egy diszperziós maradékok bármely tényező értékeket.

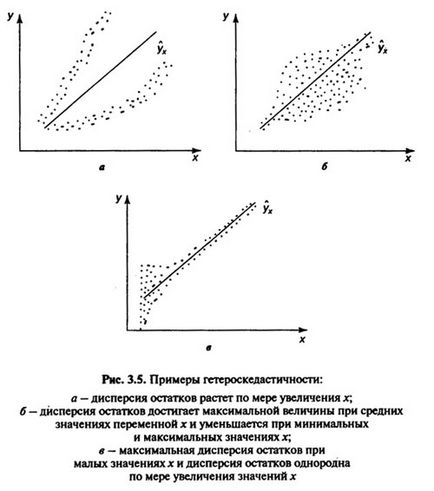
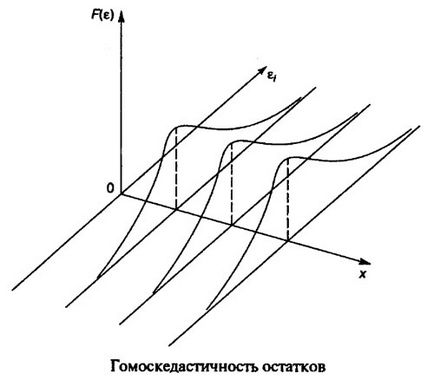
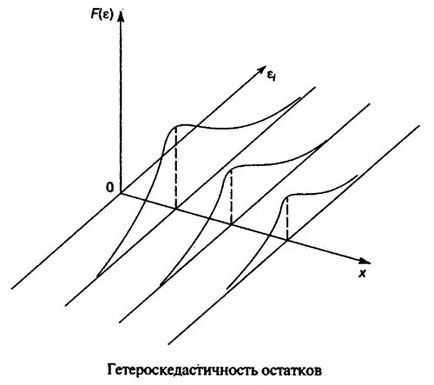
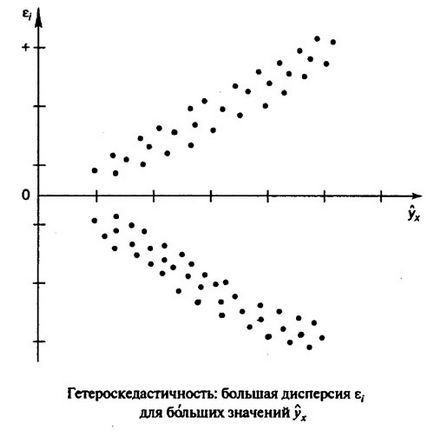
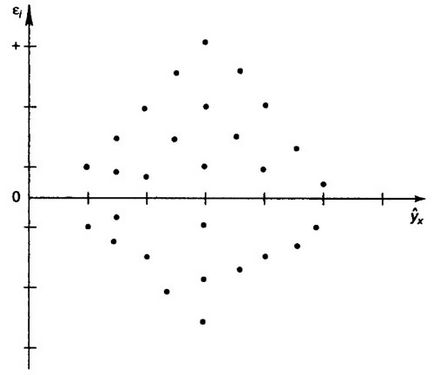
Meghatározása heteroszkedaszticitás

Egy kis minta, ami jellemző a legtöbb ökonometriai problémák. geteroskedastichosti használt becslési módszer Goldfeld - Quandt, amely 1965-ben volt, razbotan g. Goldfeld és Quandt, ahol ezeket egytényezős lineáris modell, amely a maradék diszperzió növekszik a tér a faktor. Annak megállapítására, megsértve homoszkedaszticitás, felajánlották, hogy hajtsa végre a következő műveleteket.

1. Rendezzük megfigyelés növekvő faktor X
2. Kizárni a megfontolásból központi megfigyelések C, és (n - C) 2>, ahol p - becsült paraméterek száma.
3. Osszuk a több (n - c) megfigyeljük két csoport (alacsony és magas értékek X faktor).
4. Határozza meg a maradék négyzetösszeg az első (S1) és a második (S2), és megállapította, csoportok kapcsolata: R = S1. S2.

Amikor a null hipotézist homoszkedaszticitás R arány kielégíti a kritériumokat Fischer (n - C - 2p). 2 szabadsági fokkal minden egyes maradék négyzetösszeg. Minél nagyobb az érték R meghaladja a táblázatban értéket F-teszt, annál a törött feltételezése egyenlő varianciák a maradékok.

Ahhoz, hogy egy olyan oldalra ellenőrzési megoldások econometrics kattintson ide

Kapcsolódó cikkek

• Caravan liba „(grafika)

• Rajzoló funkciókat a térben

• A grafikonok betölteni bármilyen energiafogyasztás és energiaellátó rendszer egészére, a rendelkezés