A potenciális energia kölcsönhatás
Tekintsük a rendszer két kölcsönhatásban áll egymással részecskék. Jelöljük az erő, amellyel a második részecske hat az első szimbólum F12. és az erő, amellyel az első részecske hat a második - a jelképe F21. Szerint a Newton harmadik F12 = -F21.
Tegyük fel, hogy az erő F12 iF21 van olyan értékre, amely csak attól függ, a távolság R12 és a részecskék között a részecskék mentén vannak az összekötő vonal (például gravitációs vagy Coulomb kölcsönhatás).
A fenti feltételezések alapján F12 iF21 erő is képviselteti magát
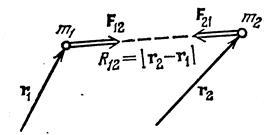
Figyelembe véve a zárt rendszer (nincs külső erők), írunk a mozgásegyenletek a két részecske:
A bal oldali az egyenlet képviseli a növekmény a kinetikus energia a rendszer idő alatt dt. jobb oldalán - a munkát a belső erők időben.
Mi átalakítsa a jobb oldalon:
Az expressziós f (R12) dR12 lehet tekinteni, mint egy növekménye függvény U (R12), amely a potenciális energia interakció:
Következésképpen az elemi által végzett munka az erő kölcsönhatása a részecskék a rendszeren belül az a potenciális veszteség kölcsönhatási energia és a növekmény a kinetikus energia a rendszer:
Ebből következik, hogy a teljes energia E tekinthető egy zárt rendszerben konzervált: De = d (T + U) = 0; E = T + U = const
A által végzett munka a belső erők, amikor a távolság a részecskék egy B határozza meg integrál:
Az utolsó kifejezést függetlennek kell lennie a munka az úton. Így, az erő függvényében csak a távolság a részecskék és irányított mentén összekötő vonal a részecskék kiderült konzervált.
A potenciális energia a kölcsönhatás a két részecske, egy adott távolságot közöttük. Ez lehet meghatározni, mint a munka erejével szemben kölcsönhatás részecskék, mozgó közülük egyet végtelenig egy előre meghatározott távolság a többi részecskék:
Belátható, hogy egy olyan rendszert, N részecskék kölcsönható potenciális energiája kölcsönhatás áll a kölcsönhatási energiák részecskék, hozott párban:
= (Faktor 1/2 az utolsó összeget jött létre, mert a választott módszer összegzése - a teljes kölcsönhatás energiája minden egyes részecske a többi - a kölcsönhatási energia minden egyes részecske pár kétszer számít).
Összegezve a korábbi eredményeket a rendszer kölcsönható részecskék, amelyek területén a konzervatív erők, megkapjuk a törvény megőrzése teljes mechanikai energia E összege a kinetikus energia a részecskék mozgását T, a helyzeti energia Uvz azok kölcsönhatása egymással és a potenciális energia Uvneshn őket a területen a külső konzervatív erők:
Ha a rendszer ki van téve, nem konzervatív erő (pl súrlódás), amelyben vállalta át a munkáját Anekonserv. majd E2 = -E1 Anekonserv