Geometriai és gazdasági jelentését a határozott integrál

A meghatározás az következik, hogy egy nem-negatív f (x) meghatározott szerves

egyenlő a területet a görbe trapéz által határolt görbe y = f (x), a vonalak az x = a és x = b, és a tengely abstsissy = 0 (4.1 ábra).

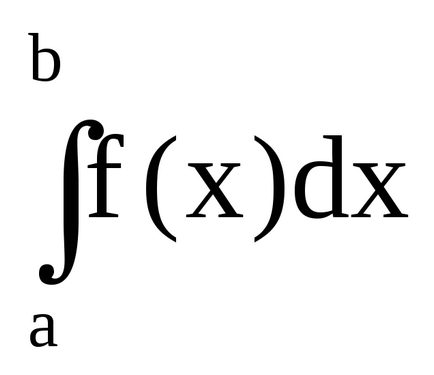
Ha a funkció - f (x) nem pozitív, akkor a határozott integrál

egyenlő a megfelelő terület görbe vonalú trapéz, együttesen a mínusz (4.7 ábra).

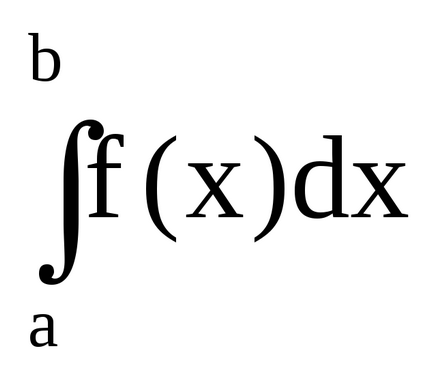
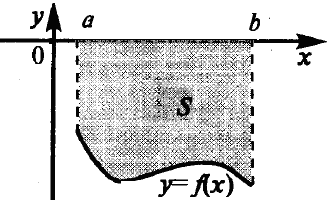
4.7 ábra - A geometriai jelentése a határozott integrál funkció nem pozitív

Egy tetszőleges folytonos függvény f (x) meghatározott szerves

Ez megegyezik a területének összege a görbe vonalú trapéz, alatt fekvő grafikon f (x), és a fenti a vízszintes tengely, kevesebb a négyzetösszeg görbe vonalú trapéz fekvő, a grafikon fölött f (x) és alatt a vízszintes tengely (4.8 ábra).

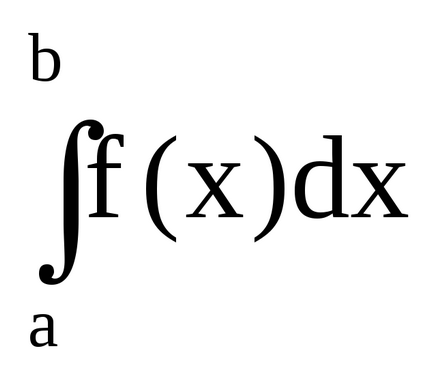
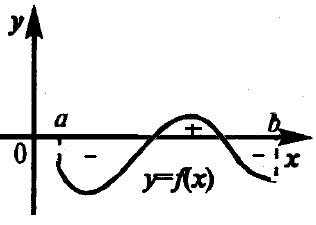
4.8 ábra - A geometriai jelentése a határozott integrál egy folytonos függvény f (x) ( „plusz” jelölt terület, ami hozzá, és a „mínusz” - az egyik, hogy kivonjuk).

Kiszámításakor a gyakorlati terület görbe vonalú formák gyakran használják a következő képlet szerint:

, gdeS- területen ábra zárt görbék közötti y = f1 (x) és y = f2 (x) az [a, b], és f1 (x) és f2 (x) - folytonos függvény definiált ebben a szegmensben az ilyen hogy f1 (x) ≥ f2 (x) (lásd. ábrák 4.9, 4.10).

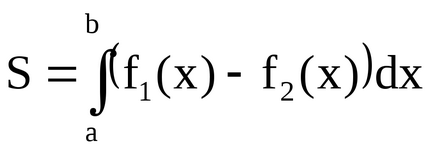
A tanuló a gazdasági értelemben vett származék, azt találtuk, hogy a származékos működik a változás mértéke a szervezet vagy folyamat idővel, vagy egymáshoz képest vizsgált tényező. Annak megállapítására, a gazdasági jelentését a határozott integrál, akkor figyelembe kell venni magának a sebességet az idő függvényében, vagy egyéb tényezők. Aztán, ahogy a határozott integrál képviseli a változást a primitív, azt találjuk, hogy a gazdaság, azt becsüli a változás az objektum (folyamat) egy bizonyos ideig (vagy bizonyos változásokat más tényezők).

Például, ha a funkció q = q (t) leírja a termelékenység attól függően, az idő, a határozott integrál a függvény

képviseli a kötet megjelent produktsiiQza intervallum ott0 1pont.

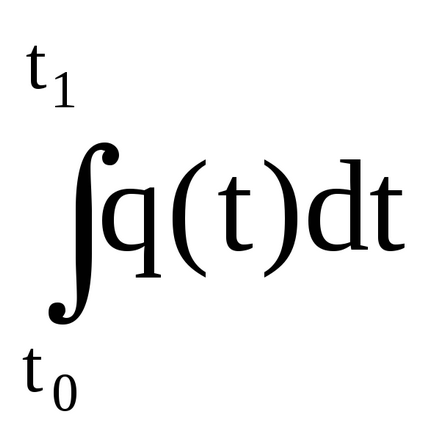
Módszerei számítási határozott integrálok alapuló módszerek korábban tárgyalt integrációs (bizonyítás nem folytat).

Amikor megtaláljuk a határozatlan integrál, használtuk a módszert a változó módosítása képlet alapján: f (x) dx = = f ( (t)) ` (t) dt, ahol x =  (t) - függvény differenciálható jelenleg intervallumban. A határozott integrál képlet a változás a változó formáját ölti

, gdei mindenki számára.

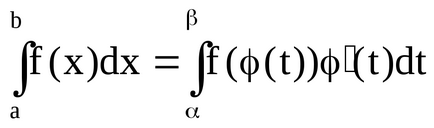
Legyen t = 2 -x 2 Togdadt -2xdxixdx = - ½dt.

Amikor x = 0 t = 2 - 2 = 0 2. Ha x = 1t = 2 - 1 = 1. Ekkor 2

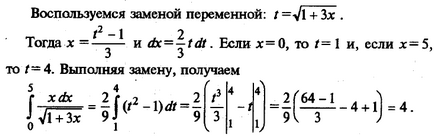
integrálás képlet a határozott integrál válik:

, hol.

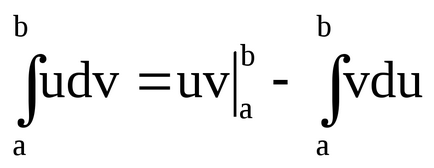
Legyen u = ln (1 + x), dv = DX. majd

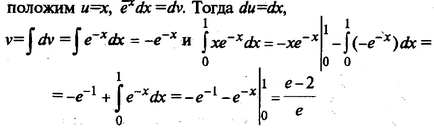
Kiszámítása területek síkidomok révén határozott integrálok

1. példa Find a terület az ábra által határolt vonalak y = x 2 - 2 és y = x.

A grafikon y = x 2 - 2 egy parabola egy minimumpont prix = 0, y = -2; abszcissza metszi pontokon

. A grafikon y = x - egy vonal felezővonala egy nem-negatív koordináta negyede.

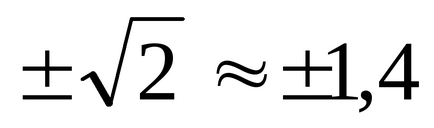
Találunk a koordinátákat a metszéspontja a parabola y = x 2 - 2 és az y = x, oldja az egyenletrendszert:

X = 2; y = 2, vagy X = -1; y = -1

Így ez a szám a kívánt területet, hogy megtalálja, lehet ábrán látható 4.9.

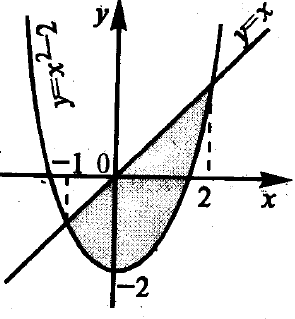
4.9 ábra - ábra vonallal körülhatárolt y = x 2 - 2, és Y = X

A intervallum [-1, 2] x ≥ x 2 - 2.

Az általunk használt formula

, feltételezve f1 (x) = x; f2 (x) = x 2 - 2; a = 1; b = 2.

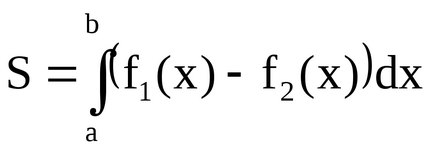
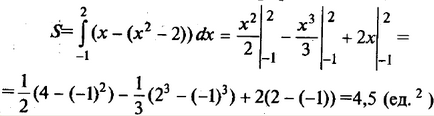
2. példa Find a terület az ábra által határolt vonalak y = 4 - és Y 2 = X 2 - 2x.

A grafikon y = 4 - X 2 egy parabola a maximális pont prix = 0, y = 4; abszcissza metszi pont 2 és -2. A grafikon a függvény az y = x 2 - 2x- parabola minimális pontban 2x- 2 = 0, x = 1; y = 1; abszcissza metszik 0 és 2.

Találunk koordinátáit metszéspontjait görbék:

4 - X 2 = X 2 - 2x

X = 2; y = 0 vagy X = -1; y = 3

Így ez a szám a kívánt területet, hogy megtalálja, akkor bevezetni a 4.10 ábra.

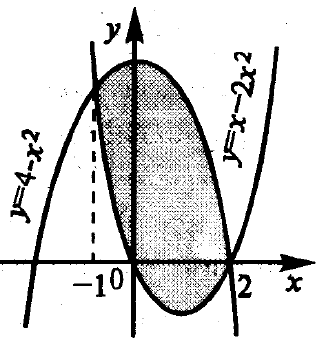
4.10 ábra - ábra által határolt vonalak y = 4 - és Y 2 = X 2 - 2x

A intervallum [-1, 2] 4 - x 2 ≥ x 2 - 2x.

Az általunk használt formula

, feltételezve f1 (x) = 4 - - x 2; f2 (x) = x 2 - 2; a = 1; b = 2.

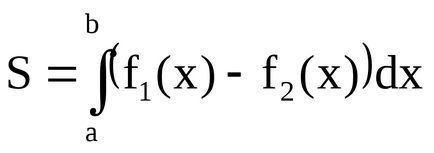
3. példa Find a terület az ábra által határolt vonalak y = 1 / x; y = 2 x = 4 és Y koordináta-negyede nem negatív.

A grafikon a függvény y = 1 / x egy hiperbola, a pozitív x konvex lefelé; koordináta tengelyek aszimptotákkal. A grafikon a függvény az y = x 2 nemnegatívak koordináta negyedévenként - a parabola ága minimális pont a származási. Ezek a grafikonok keresztezik 1 / x 2 = x; x 3 = 1; x = 1; y = 1.

Egyenes y = 4, egy grafikon a függvény y = 1 / x keresztezi az x = 1/4, egy grafikon y = x 2, x = 2 (vagy -2).

Így ez a szám a kívánt területet, hogy megtalálja, lehet ábrán látható 4.11.

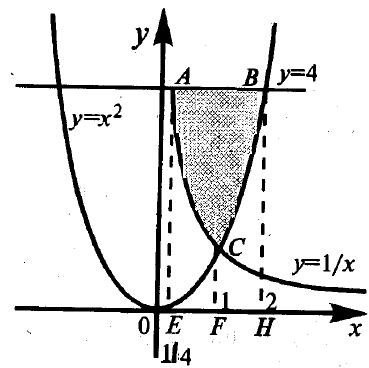
4.11 ábra - ábra által határolt vonalak y = 1 / x; y = 2 x = 4 és Y koordináta-negyed nem negatív

Kedvelt ABCravna kitalálni Avenay terület közötti különbség egy téglalap területét, amely 4 * (2 - ¼) = 7, és az összeget a két négyzet és ívelt trapézokkal ASFE SVNF. Számítani a területen ASFE:

Számítani a területen SVNF:

.

Így a szükséges terület 7 - (LN4 + 7/3) = 14/3 -ln43,28 (2 db.).