A hőkapacitása szilárdanyag

Home | Rólunk | visszacsatolás
Termikus tulajdonságok A szilárd anyagok
Bármely hőmérsékleten szilárd atomok alávetni termikus ingadozások. Amikor egy szilárd fűtőtest növeli a rezgési energiát az atomok, és az atomok energiát bocsátanak ki, amikor egy szilárd test hűtés. Törvények abszorpciós és emissziós hőenergia jellemzi hő.
A moláris hőkapacitás számszerűen egyenlő az energia, amelyet az anyag, ha melegítjük 1 ° C-on
1819-ben g. Dulong és Petit kísérletesen létrehozott amely szerint a fajhője szilárd anyagok magas hőmérsékleten állandó, és egyenlő a 25 J / mol × K vagy 3R.
Szerint a klasszikus fizika, hőenergia egyenletesen oszlik el a szabadsági fok :. Minden atom három szabadsági fok és jellemzi összenergia a kinetikus energia, plusz a potenciális energia. Egy egyetlen atom. 1 mol anyag tartalmaz NA atomok, akkor annak átlagos hőenergia E = 3NA kT.
Azonban alacsony hőmérsékleten, Dulong és Petit törvény nem működik (ábra. 6.1), és ezt meg kell magyarázni.
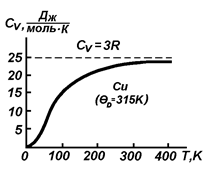
Ábra. 6.1. Hőmérsékletfüggése fajhője szilárd
A hőkapacitása szilárd anyagok.
1. Einstein modellje.
1907-ben Einstein alapján azt a hipotézist, Planck, javasolt az első modell magyarázza az alacsony hőmérsékletű fajlagos hőguta. Azt javasolta:
1) Szilárd - egy sor hasonló harmonikus oszcillátor (atomok), hogy oszcillálnak függetlenül ugyanazon a frekvencián w három egymásra merőleges irányban.
2) Az energia az oszcillátorok Planck kvantálva.
a) Magas hőmérséklet: (exp számlálója hajlamos 1, expandált számban) a nevezőben exp. A törvény a Dulong és Petit:
b) Alacsony hőmérséklet:
Az ok - az egyenlőtlen energia felett szabadsági fokkal, azaz a .
Azonban Einstein modell nehezen egyeztethető össze a kísérlet (ábra. 6.2).
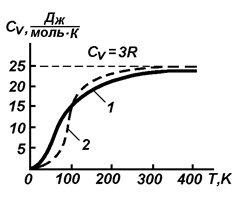
Ábra. 6.2. Összehasonlítás számítások szerint az Einstein modell (2) A kísérleti függőség (1).
Debye (1912) figyelembe vette a jelenlétét a szilárd a különböző üzemmódok a normál rezgések.
Ezután, egy egységnyi térfogatú (5,50) keresztül w:
Q Debye jellemző hőmérséklet határozza meg a határfrekvencia wD. megfelelő korlátozó érték a hullám vektor kD a Brillouin zónában, azaz amikor Debye izgatott egyáltalán lehetséges természetes rezgések a kristály. A fázis térben hullám vektorok kD értéket társított teljes N számának rezgések állapot:
ahol (2p) 3 - k -space mennyiség tulajdonítható 1 hullám vektor.
Ettől. egy p-térfogata egyenlő h 3. K-térben -Pro - (2p) 3.
a) Magas hőmérséklet:
b) Alacsony hőmérséklet:
Cseréje határait integráció:
Ez az eredmény jó egyezést mutat a kísérlet T
0 és K jelentése jobb, mint Einstein modell magasabb hőmérsékleten (ábra. 6.2).
Egyes értékei q félvezetők táblázatban mutatjuk be a 6.1.