Euler függvény
Euler függvény φ (a) határozza meg az összes természetes számok és a szám a természetes számok kölcsönösen prime egy. és nem haladja meg a. Feltételezzük, hogy φ (1) = 1. Ez a funkció kerül kiszámításra az alábbi képlet szerint
ahol
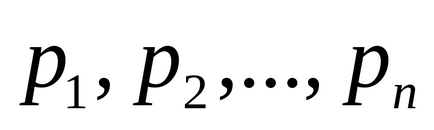
A számok számának alkotó azonos φ (m) a redukált maradékot rendszer.
A közös tulajdon teljes és csökkentett rendszer maradékok
Ha a számok
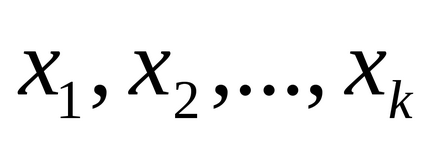
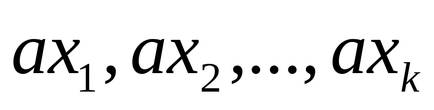
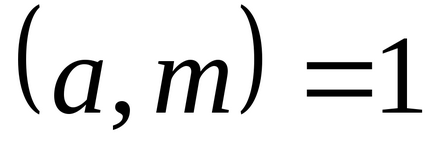
Mutassuk meg, hogy a szám 25, -20,16,46, -21,18,37, -17 alkotnak egy teljes rendszert maradékok modulo 8.
Mi egy teljes rendszer a legkevésbé nem-negatív számok
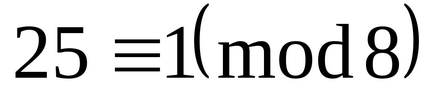
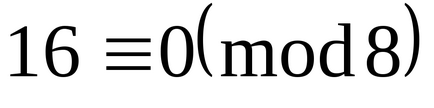
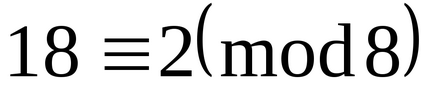
Tehát ezek a számok 0,1,2,3,4,5,6,7 alkossanak meg a maradékok modulo 8-rendszer.
Euler és Fermat-tétel
Legyen x fut keresztül a redukált maradékrendszer
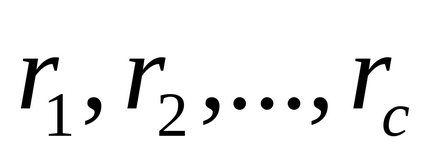
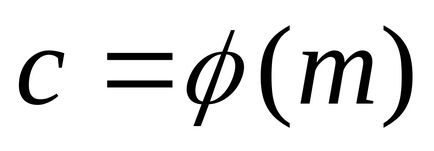
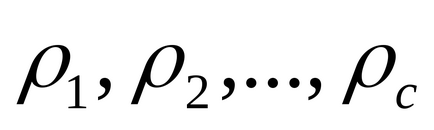
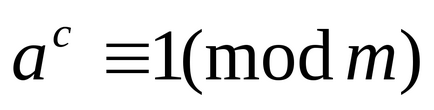
Egy egyszerű p és a. nem osztható p-vel. van
Ez a tétel egy speciális esete Euler-tétel, ha m = p. Tól (2) meg lehet könnyen beszerezni egy nagyon fontos összehasonlítás
,
teljesül minden egész számokat. ez igaz a többszöröse p.
Ellenőrizze Euler-tétel egy = 5 és.
,
.
Keresse meg a fennmaradó osztódó
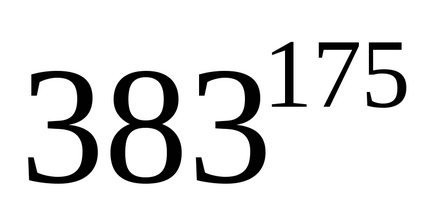
Mivel akkor. mert
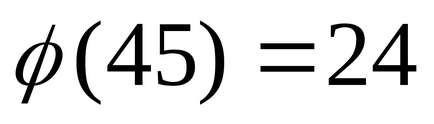
.
A: A kívánt egyenleg 32.
Az összehasonlítás az első fokú (problémamegoldás)
Problémák módszer Euler összehasonlítása. Ellenőrizze a helyes választ helyette.
(3,5) = 1, akkor ez az összehasonlítás egy egyedülálló megoldás (a számokat tekintve osztály X modm). Szerint a Euler formula van,
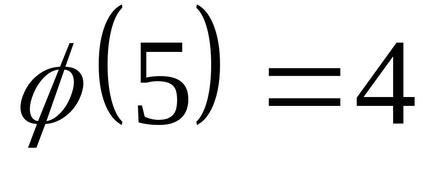
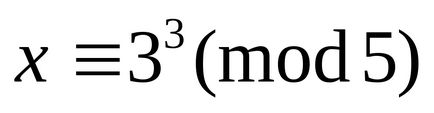
Problémák módszer Euler összehasonlítása.
(5.10) = 5, 7, de nem osztható 5, tehát ez az összehasonlítás nem megoldásokat.
Problémák módszer Euler összehasonlítása.
Mivel (25,17) = 1, akkor ez az összehasonlítás van egy megoldás. Ez az összehasonlítás egyenértékű az összehasonlítás. Szerint Euler-képlet van.
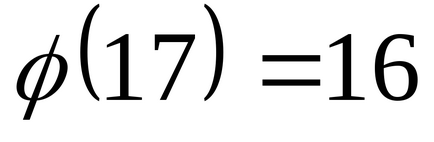
.
Döntse egyik módja az összehasonlítás
(12,15) = 3. Ennélfogva ez az összehasonlítás 3 oldatok (abban az értelemben, az osztályok). Vegyünk egy összehasonlítás
amely nyert e csökkentés után 3.
Szerint Euler-képlet, van,.
Találtunk egy megoldást a kongruencia (2). összehasonlítjuk az oldat (1) adja meg, k = 0,1,2.
; ; .
Tulajdonítható, hogy a jogot, hogy a szám 523 a három számjegy a kapott hatjegyű szám osztható 7,8,9.
Hagyja hátterében számos x. majd otkudaili. Znacheniex egy háromjegyű szám a t = 0 és t = 1. kap
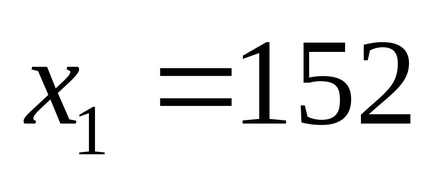
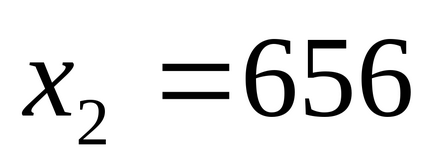
523.152 osztva 7,8,9;
523.656 részvények 7,8,9.