szabályos sokszög
Szabályos sokszög - a konvex sokszög. amelyben az összes oldal egyenlő egymással, és a szögek közötti szomszédos oldala egyenlő.
Meghatározása egy szabályos sokszög függhet a meghatározása a sokszög. ha úgy értelmezzük, mint egy lapos zárt sokszög, akkor ott van a meghatározása a megfelelő csillag sokszög, mint egy nem-konvex sokszög, amelyben minden oldalról mindig egyenlő, és minden a szögek egyenlő egymással.
koordináták
Legyen x C> és y C> - a középpont koordinátáit, és az R - a sugara a szabályos sokszög kerülete köré. # X03D5; 0 _> - szögkoordináta az első vertex, akkor a derékszögű koordinátái a csúcsai egy szabályos n-szög által megadott képletek:
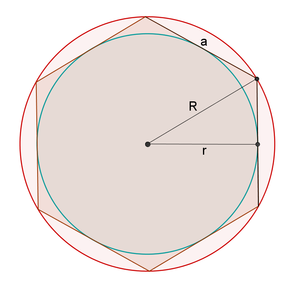
Szabályos sokszög beírt és körülírt kerülete körül
Legyen R - sugara a szabályos sokszög kerülete körül. Ezután a sugara a beírt kör
és az oldalsó hossza a sokszög egyenlő
A terület egy szabályos sokszög n számú oldallal, és a hossza egy oldalon:
A terület szabályos sokszög több oldalról n. írt körön R. a következő:
A terület szabályos sokszög több oldalról n. körülíró egy r sugarú kör. a következő:
A terület egy szabályos sokszög egy oldalainak száma értékét visszaállítja az n
ahol r - távolság a középpont felé a központ, egy - oldal hossza.
A terület egy szabályos sokszög fölött a kerület (P) és a sugara a beírt kör (R) jelentése:
Ha szükséges kiszámítani a oldalhosszúságú (n) n-szög pontosan helyezhető be egy kör, tudva kerületi hossza (L) ki tudja számítani a hosszát egyik oldalon a sokszög:
a n> - a hossza az oldalán szabályos n-szög.
ahol n száma a sokszög oldalainak.