Komi probléma az egyenlet teploproodnosti - studopediya
Tekintsük a homogén hőegyenletre.
Ennek hiányában a külső hőforrás. Mi jelent a probléma a Komi:
Find függvény U (x, t) kielégíti a következő egyenletet:
A fizikai értelmében a probléma - a meghatározása egyenletes hőmérsékletet a végtelen web bármikor az ismert. hőmérséklete a kezdeti t = 0 időpontban.
Úgy véljük, hogy áramot. szigetelt felületén a rúd (a hő nem megy el a rúd)
Most tételezzük fel, hogy a függvény U (x, t), és elegendően sima funkciók csökkenő
Olyan gyorsan, hogy a lények. Átalakítja. Fourier
A Fourier-transzformáció a függvény változásokat. H.
2. törvény eltérés működését.
Következésképpen azt találjuk, hogy átalakítja. Fourier második deriváltja társított funkciót a Fourier transzformációs maga következő funkciókat. egyenlőség
Alkalmazandó konvertálja. Fourier, hogy az eredeti egyenlet és koldulni. körülmények között. csökkentve üzenet. a probléma, hogy a Cauchy probléma egy közönséges differenciálegyenlet
Az első egyenletrendszer marad:
A kapott probléma komi feladata közönséges differenciál. Eq.
A megoldás erre a problémára az a függvény
(Amely lehet ellenőrizni az egyszerű helyettesítés)
Megmutatjuk, hogy a funkció
a Fourier-transzformáció
Ie yavl. Átalakítja. Fourier-sor funkciók:
Bebizonyítottuk, hogy a függvény
A megoldás felírható:
Mint jól ismert termék két Fourier transzformáció = konvolúciós Conversion. funkciók megváltozik. Fourier transzformált konvolúcióval funkciók
A megoldás az eredeti Cauchy probléma említett. Poisson-féle képlet a megoldás a hő egyenlet Cauchy problémát.
Továbbra is, hogy ellenőrizze, hogy az előre meghatározott egyenletet kielégíti a kezdeti feltétel, azaz
Ha úgy találja, hogy
A kapott oldatot megfelel annak a feltételnek:
Az alapvető megoldás a hő egyenlet (- Dir funkció)
A képlet nazyv Poisson. alapvető fontosságú. oldatot a hő egyenlet.
Figyelembe véve függvényében az érvek x, t kielégíti hőegyenletre
mint látható ellenőrzése.
Az alapvető megoldás egy fontos fizikai jelentése kapcsolatos koncepció a termikus impulzus. Tegyük fel, kezdetben a kezdeti hőmérséklet-eloszlást adja meg:
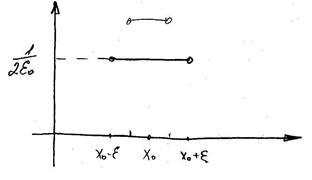
Minél kisebb a magasabb polcon
Ezután alapján Poisson eloszlású. a hőmérséklet a rúd formájában:
A középérték tétel van egy pont
. ahol hagyjuk. majd az utolsó egyenlőség megkapjuk
- Ez azt jelenti, hogy a funkció a hőmérséklet eloszlása a bárban idején. Ha a kezdeti idejét x0 végtelen csúcs hőmérséklet és a többi pont a rúd hőmérséklet egyenlő a 0. Ez volt a kezdeti hőmérséklet eloszlás lehet közelíteni. végrehajtása az alábbiak szerint:
Időpontban, hogy a pont X0 rúd egy nagyon rövid idő alatt a láng hozta nagyon keskeny, magas hőmérsékletű (hő impulzus) - ez a kezdeti hőmérséklet-eloszlás a készletek. Dir képlet és jelezte. Nem yavl. függvény a szokásos értelemben vett funkció határozza hivatalosan a kapcsolat
2. az egyes intervallumok. tartalmaz. x0
Így az alapítvány. yavl döntést. oldatot rúd egyenlet egy kezdeti hőmérséklet-eloszlás