Cauchy probléma hőegyenletre - a problémák megoldását az ellenőrzés
Cauchy probléma hőegyenletre





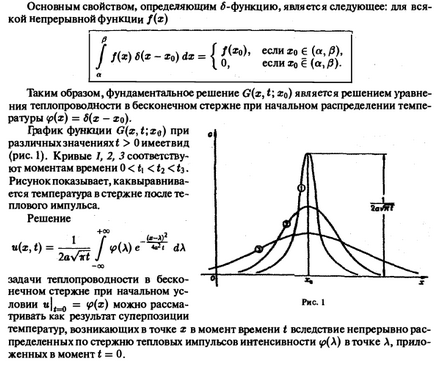
Tekintsük a homogén egyenletet megfelelő esetén hővezető. források hiánya. A Cauchy problémát jelent az alábbiak szerint: találni egy funkció t), kielégíti a következő egyenletet, és a kezdeti feltétel a Cauchy probléma hőegyenletre fizikai értelmében a probléma abban áll, hőmérséklet meghatározásának homogén végtelen rudat bármilyen időpontban az ismert hőmérsékletet az idő. Úgy tartják, hogy az oldalsó felülete a rúd hőszigetelt, így rajta a hő a rúd nem hagy. M Tegyük fel, hogy kellően sima funkciók ubyvayuyute át x2 + t2 +00 olyan gyorsan, hogy a Fourier-transzformáció meglévő 2) jogszerű differenciálódás Ezután, alkalmazva a Fourier-transzformáció, hogy mindkét oldalán az egyenlet (1) és állapota (2), a feladat (1 ) - (2) át a Cauchy probléma közönséges differenciálegyenlet (a értéke £ szerepét játssza a paraméter). Az oldatot (5) - (6) formájában van Már korábban megállapították, hogy ha a Fourier-transzformáció. Ezért, feltételezve t = kap Így leírható mint egy bal oldalán (8) van a Fourier transzformáltja a jobb oldali (7) egyenlet van a termék a Fourier transzformálja a funkciók segítségével a konvolúciós tétel, amely szerint az egyenlőség (7) (a x argumentumot ) az ismeretlen funkciójú u (x, t). így a (8) képletű átírható, mint: ahol, a kifejezés a konvolúciós függvény 4> (x) R s, kaptunk képletű oldatot ad az eredeti probléma (1) - (2) a szerves Poisson. Valójában, ez lehet mutatni, hogy bármely folytonos függvény korlátos IPT), képlet által meghatározott (9), bármilyen sorrendben deriváltak X és t t> 0, és kielégíti az (1) egyenlet esetében t> 0 és Vx. Megmutatjuk, hogy a funkciója megfelel a kezdeti feltétel. Ezután rakjuk úgy mint amikor mi kap, mert megfogalmazni a következő fontos eredmény. 1. Tétel A osztály műveleteit korlátos megoldást Cauchy probléma (1) - (2) egyedi, és függ folyamatosan a kezdeti funkciót. Példa. Találjanak megoldást Cauchy probléma Cauchy probléma hőegyenletre miközben kihasználják a Poisson formula (9) megkapjuk Proobrazuem szerves jobb a becsület. Meg kell változtatnunk változók Aztán intefal a jobb oldalon az egyenlet formájában (I) képlet (Itt vospoleov leltár, hogy megkapjuk a / Ezért a megoldás arra a problémára, a határ, és tsya formula Lelia látni, hogy a beépített novemberében a funkció u ( x, f) megfelel a kezdeti feltétel (2 „). Egy azonnali ellenőrzés könnyen ellenőrizheti, hogy a ata funitsiya a egyenletnek felel SautWtl. tól Poisson képletű (9) Ebből következik, hogy a hő rasorosgranya etsya rúd mentén azonnal. Valóban, feltételezzük, hogy a kezdeti hőmérséklet) pozitív on és nulla kívül intervallumban. Ezután a későbbi forgalmazás hőmérséklet jutunk el látva, hogy a tetszőlegesen kis t> 0 tetszőlegesen nagy | x | van tt (x, t)> 0. A obyas kyaetsya pontatlansága elméleti feltevések származtatására az egyenlet a hővezetés. figyelmen kívül hagyva yushih gerinc tehetetlenségi mozgása molekulák. Mindazonáltal az egyenlet a hővezetési ad egy jó mennyiségi megállapodás kísérletet. A pontosabb leírást a hőátadási folyamatokat adják az úgynevezett közlekedési egyenletek. 2.1. Az alapvető megoldás a hő egyenlet funkciót tartalmazza a Poisson (9) képletű nevezzük az alapvető megoldás a hő egyenlet. Tekinteni, mint egy függvényében érvek x, t, ez kielégíti az egyenletet u = a2ihh, amint azt a közvetlen ellenőrzést. Az alapvető megoldás egy fontos fizikai jelentése kapcsolatos koncepció a termikus impulzus. Tegyük fel, hogy a kezdeti eloszlása ip (x) a hőmérséklet a következő: Ezután a (9), a hőmérséklet-eloszlás és a rúd megjelenés a középérték tétel, amely már halad ez az egyenlőség a limit, mint az e - * 0, azt kapjuk, Ez azt jelenti, hogy a G funkció (x, t \ HO) a hőmérséklet-eloszlást a rúd idején t> 0, ha a kezdeti t = 0 időpillanatban az x = XO volt végtelen hőmérsékletű csúcs (e - * 0, a funkció 4> et; xa) at különböző értékei t> Oimeetvid (ábra. 1). Görbék 1, 2, 3 felelnek időpillanatok • ábra mutatja kakvyravniva etsya rúd utáni hőmérséklet a hő impulzus. A megoldás a Cauchy probléma a hővezetési egyenlet hővezetési probléma egy végtelen rúd kezdeti feltétel lehet tekinteni, mint az eredménye hőmérséklet szuperpozíció előforduló azon a ponton x t időpontban miatt folyamatosan eloszlatunk a rúd mentén hő impulzusokkal y> (A) az A pont, alkalmazva a t időpillanatban = 0.