Hogyan lehet megtalálni a területen egy kör, négyzet, háromszög

Hogyan lehet megtalálni a terület a kör?

Kerülete - zárt síkgörbe amelynek minden pontja egyenlő távolságra van egy adott pont (központ) fekvő ugyanabban a síkban, mint a görbe.
Kör - része a sík által határolt kör.
Radius - vonalszakasz, amely összeköti a közepén a kör egy pont az ő, valamint a hossza ebben a szegmensben. Általában oboznachaetsyaR.
Átmérő - egy összekötő szakasz a pár legtávolabbi egymástól kerületileg pontok, és a hossza és ezen intervallum. Átmérő mindig áthalad a közepén a kör. Általában oboznachaetsyaD ILIO. Átmérő kétszeresével egyenlő kör sugara: D = 2R, R = D / 2.

Az arány a kerülete, hogy átmérője azonos minden kerületére. Ez a kapcsolat egy transzcendens szám, amely jelöli a görög betű pi: π = 3,14159.

Hogyan lehet megtalálni a háromszög területe?

Triangle - egy lapos geometriai alakzat által határolt három hosszúságú pár egymást metsző vonalak. A metszéspontok nazyvayutsyavershinami treugolinika és általában által kijelölt tőke latin betűkkel: A, B, C Velichinyuglov a csúcsai, amelyek metszik a megfelelő vonalak általában jelöljük a görög betűkkel: α, β, γ. A átellenes sarok vonalszakaszok végeit összekötő háromszög nazyvayutsyarebrami (oldalai) a háromszög és a kijelölt rendre a, b, c.

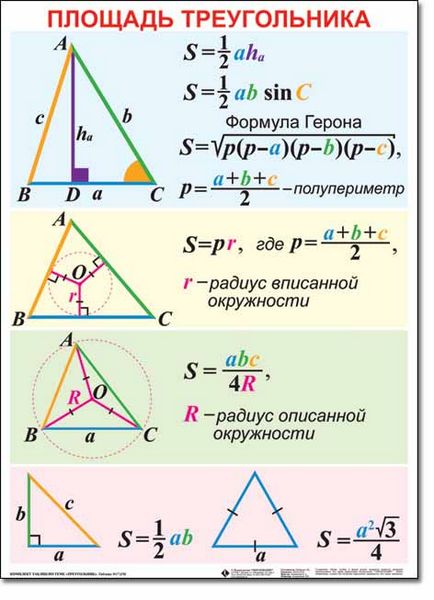
Az alábbiakban képletek, amely megtalálható az S felület a háromszög csúcsai A, B, C, a megfelelő értékeket a szögek, β, γ és ellentétes oldalain közülük a, b, c:

S = a • b · sin (γ) / 2 = a · c · sin (β) / 2 = b · c · sin (α) / 2,

S = a 2 · sin (β) · sin (γ) / (2 · sin (β + γ),

S = √ (P · (p - a) · (p - b) · (p - c)) (Heron-képlet), ahol √ (.) - kijelölése a négyzetgyök, p = (a + b + c) / 2 - semiperimeter háromszög.

S = a • ha / 2 = b · HB / 2 = C · hc / 2. ahol ha - magassága csökken egy csúcsa, hogy az oldalán egy, HB - a csúcstól B oldalra b, HC - a C csúcsból a c oldal.

S = R · p. ahol r - a sugara a beírt kör, p = (a + b + c) / 2 - fél-kerülete a háromszög.

S = a • b · c / 4R, ahol R - a kör sugarát körülírt körül a háromszög.

Ha derékszögű koordináták megadott pontok a síkban A (. X1 Y1), B (. X2 Y2) és a C (. X3 y3), az S felület megtalálható a következő egyenlettel (determináns révén másodrendű mátrixok koordináta különbségek):

S = | (x1 - x3) · (y2 - y3) - (x2 - x3) · (y1 - y3) | / 2. ahol |. | - kijelölése a modult. Ez a képlet származik a kifejezés a vektor termék a két vektor egy síkban, ami a nagysága egyenlő a meghatározója a koordinátáit.

Hogyan lehet megtalálni a terület a derékszögű háromszög?

Ez az úgynevezett derékszögű háromszög. az egyik sarokban, amely 90 ° -os (a jobb oldalon). Mivel az összeg a háromszög szögeinek 180 °, derékszögű háromszög lehet, hogy csak egy.

Az alábbiakban képletek kiszámításához a képlet S. spetsificheskikie terület négyszögletes háromszögek. Jelmagyarázat: A - hossza átfogója (a szemközti oldalon a derékszög), a. b - hossza a lábak (a fél szomszédos a megfelelő szögben), α. β - ezek a mennyiségek befogó szemközti szöge (α + β = 90 °).

Két befogó: S = a • b / 2

A befogó és a átfogója: S = a • sqrt (c 2 - a 2) / 2 = b · sqrt (c 2 - b 2) / 2.

ahol sqrt (.) - kijelölése a négyzetgyök

H ow, hogy megtalálják a terület a tér?

Tér (a latin quadratus -. Négyszögletű) - jobb oldali szögletes, amely az összes oldalai és szögei egyenlők. Lehet meghatározni, mint egy téglalap, amelynek két szomszédos oldala egyenlő egymással, vagy egy rombusz, amelyben az összes szög derékszög.

Symmetry. A tér a legmagasabb szimmetria között négyszögek. Meg:

• Négy két-szeres szimmetriatengelye (síkidom, amely egyenértékű reflexiók), amelyek közül kettő kiterjeszti átlói mentén egy négyzet, és a másik két - párhuzamos oldala;
• egy negyedik szimmetriatengelye (közepén áthaladó egy négyzet a síkjára merőleges).

Átlós. A tér két átlója összekötő nem szomszédos csúcsot. Négyzet átlójának a szögfelezői szöge metszik egymást a tér közepén derékszögben egymáshoz, és ossza ketté. Minden átlós osztja a tér két egyenlő szárú derékszögű háromszögek. Két átlója együtt osztja a tér négy egyenlő szárú derékszögű háromszög.

Jelöljük az oldalán a tér egy. a hossza a D átló szerint számítjuk a Pitagorasz-tétel:

Beírt és körülírt körök. Négyzetbe írt kör érinti a tér közepén, minden oldalról, és egy r sugarú. felével egyenlő oldalán a tér egy. Leírunk egy négyzet kerülete mentén halad végig a csúcsait, és van egy R sugarú felével egyenlő hossza a diagonális egy négyzet d:

Kerület és terület. Kerület P tér hosszának összegét a négy oldala van. A terület S egyenlő a tér a tér a hossza az oldalán:

P = 4a = 8r = 2√2 · R,
S = a 2 = 4r 2 = 2R 2.

Hogyan lehet megtalálni a területet a trapéz?

Trapéz - négyszög, amelyben két párhuzamos oldala (bázis a trapéz), míg a többiek - nem párhuzamos (laterális oldalán a trapéz). Összekötő szakasz közepén a fél, az úgynevezett középső sor a trapéz.