Egyenlőtlenség aritmetikai és geometriai algebra
Egyenlőtlenség aritmetikai és geometriai (Cauchy)
A számtani középértéke n pozitív számok nem kevesebb, mint a geometriai átlag.
sőt, az egyenlőség elérjük akkor és csak akkor
A speciális esete ennek az egyenlőtlenség, amely összeköti a számtani átlag és mértani átlaga két pozitív szám, ősidők óta ismert. Leggyakrabban ez bizonyult a geometriai értelmezést.
Készítünk egy kör átmérőjű AB = a + b.
Egy tetszőleges C pontot a kör átmérője tart CD merőleges.
By ingatlan derékszögű háromszög magassága által végzett átfogója. a geometriai átlag, a nyúlványok közötti a lábak a átfogója:
Csatlakozás C pont középen kör pont O. CO - sugara, így felével egyenlő átmérő:
azaz a hosszukat CO a számtani átlaga a és b.
Egy derékszögű háromszög COD CD - láb, CO - átfogója.
Mivel az átfogó mindig nagyobb, mint a lábát. CO> CD, tehát a számtani a és b nagyobb, mint a geometriai átlag.
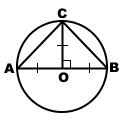
Ha AO = BO, azaz a = b.
(Mivel a> 0), és a Q és ebben az esetben a számtani átlaga az A és B azonos a geometriai átlag őket.
Így a számtani átlaga pozitív számok a és b nem kevesebb, mint a geometriai átlag.
QED.
Általában az egyenlőtlenséget bizonyította Cauchy.