Túlzó, a különcség, az igazgatónő és a asymptote

A hiperbola a pályája pont a síkon, amelyek mindegyikére abszolút értékének különbsége távolságot két pont és az adatok síkban. az úgynevezett gócok, állandó érték egyenlő 2a.

A távolság a foci - 2c.

Ha a tengelyek a Descartes-féle koordináta-rendszer úgy választjuk, hogy a gócok a hiperbola található az x tengely a szimmetrikusan a származási (ábra. 2.13.1), a kanonikus egyenlet a formája a hiperbola

Ahol. Az egyenlet a formában (2.13.1) nevezzük kanonikus egyenlete hiperbola. Ezzel a választott koordináta-rendszer, a koordináta-tengelyek szimmetriatengelye a hiperbola. és az eredete - a közepén szimmetria. Ox tengely nevezzük valós tengelyen. és Oy - a képzetes tengelyének túlzás. A metszéspontok a tengelye a hiperbola csúcsoknak nevezzük a hiperbola.

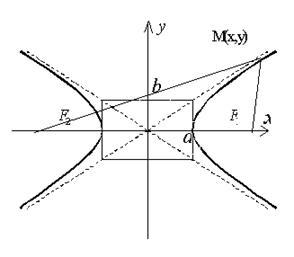
Téglalap oldala a 2a és 2b. szimmetrikusan helyezkedik tengelyéhez viszonyítva a hiperbola, és viszonyítja a csúcsot, az úgynevezett alap téglalap hiperbola. Főátlójában a téglalap (végtelenül folytatás) aszimptotái hiperbola és leíró egyenletek

Excentricitás hiperbola (például ellipszis) az a szám. ahol a - távolságra a központtól, a hiperbola a tetejéig. Nyilvánvaló, hogy minden hiperbola e> 1.

Ha M (x; y) - tetszőleges pontja hiperbola, a szegmensek nevezzük fokális sugarai M pontban fokális sugarai a jobb oldali ág a hiperbola alapján lehet kiszámítani, hogy a képletek és. Focal sugarak a bal ág túlzás - a képletek és.

Ha hiperbola adják (2.13.1), akkor a vonalak által meghatározott egyenletek. nevezzük directrices.

Az egyenlet a hiperbola, amelynek gócok fekszenek az x tengely körül szimmetrikusan eredetét, ha a pont fekszik a túlzó aszimptotákkal és ismert egyenlet.

Az egyenletek aszimptotákkal megtalálni. vagy. Mivel a pont tartozik túlzás, a koordinátái kielégítik az egyenletet (2.13.1). vagy hol. Ezért találunk. akkor. így, az egyenlet formájában egy hiperbola.

Tekintettel arra, túlzó. Helye ellipszis a és b. foci, különcség, asymptote egyenlet.

Azt ossza mindkét oldalán az egyenlet így 144. Tehát a = 3, b = 4, így a tengely a hiperbola rendre 6, és a 2a = 2b = 8. Ettől. A gócok hiperbola vannak a pontok és. Excentricitás hiperbola az alábbi képlet szerint. Összhangban (2.13.2) aszimptotákkal egyenleteknek formájában :.

Parabola, annak igazgatónő

A parabola a pályája pont a síkon, amelyek mindegyikére a távolság fix pont F. úgynevezett fokális síkban. egyenlő távolságban rögzített egyenes vonal, az úgynevezett direktrixét.

Legyen adott egy parabola. Egy derékszögű derékszögű koordináta-rendszert úgy, hogy az x-tengely áthalad a hangsúly a parabola és merőleges a direktrix a direktrix került a tekintett fókuszpontba irányított. A származási félúton található a fókuszt és direktrixét (ábra. 2.14.1). Ebben a koordinátarendszerben, ez parabola határozza meg a következő egyenletet:

ahol p - a távolság a fókuszt direktrixét (parabola paraméter). Egyenlet (2.14.1) a kanonikus egyenlete parabola.

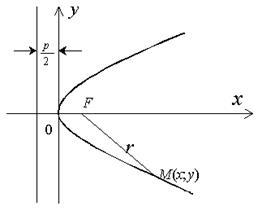
Direktrix a parabola egyenlet által definiált. Focal sugara egy tetszőleges M pont (x; y) a parabola lehet kiszámítani a következő képlettel

A parabola van egy szimmetriatengelye, az úgynevezett tengelye a parabola, amely metszi egy ponton. Az a pont, ahol a parabola metszi a szimmetriatengely, az úgynevezett csúcsa a parabola. Ha a fenti koordinátarendszerben adja meg a parabola tengelye egybeesik a vízszintes tengelyen a csúcs a származás, és az egész parabola rejlik a jobb fél síkon.

Ha a tetején a parabola (2.14.1) mozgassa a pontot. akkor a kanonikus egyenlet.

Keresse meg a fókusz F és az egyenlet a direktrix a parabola.

A paraméter az e parabola p = 12. Mivel a távolság a fókuszt direktrixét egyenlő. a hangsúly a koordinátái F (6, 0). és az egyenlet a direktrix. azaz X + 6 = 0.

Készítsen egyenlet parabola csúcsa az origó, és egy pont fókuszban F (0, 8).

Mivel a hangsúly a parabola fekszik az y tengelyen, és a csúcs - a származás, az egyenlet a parabola lehet írni. Mivel a hangsúly a koordináta negatív, akkor az egyenlet a parabola kell törekedni formájában.

A fókusztávolság. ahol 2p = 32. Ezért az egyenlet formájában egy parabola.