Aszimptota a görbe, a problémamegoldás a matematika és egyéb tárgyak.

A koncepció kerül bevezetésre aszimptotákkal a görbék grafikonon (vagy egyedi grafika ág) tart a végtelenbe. Ez lehet, ha a funkció nem korlátozott, illetve ha be van állítva a korlátlan intervallum.

Definíció. Az egyenes vonal az úgynevezett aszimptotájának a görbe, ha a távolság a görbe az egyenes vonal nullához, mint az a pont tart végtelenbe.

Példa 1. Igazoljuk alkalmazásával aszimptotákkal meghatározása, hogy a vonal aszimptotájának a görbe.

Határozat. A definíció szerint a asymptote. A mi esetünkben.

Három fajta aszimptotákkal: függőleges, vízszintes és ferde.

Az egyenlet bármilyen függőleges vonal, azaz a párhuzamos egyenes tengelye a forma.

Ha a vonal a függőleges aszimptotájának a grafikon, akkor nyilvánvaló, hogy legalább az egyik az egyoldalú határértékek vagy egyenlő a végtelenig (vagy).

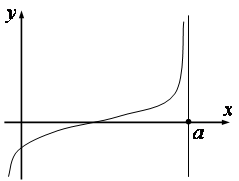
Minden funkció végtelen folytonossági (rések a második fajta) van egy függőleges asymptote.

Példa 2. Keresse meg az egyenletet a függőleges aszimptotáját a grafikon funkciók.

Határozat. Látjuk, hogy ha inkább ez egy egyenes vonal a függőleges aszimptóta és kétoldalú.

Minden vízszintes vonal van az egyenletnek.

Ha a vonal vízszintes aszimptotája a görbe, akkor.

Példa 3. Keresse meg a vízszintes aszimptotáját a görbe.

Határozat. Azt találjuk, hogy van, mikor és, majd egyenesen - vízszintes aszimptotája a görbe.

Meredeksége aszimptóta egyenlet általában olyan formában. A definíció szerint a asymptote vagy

Elosztjuk mindkét oldalát:

A létezését a lejtőn a aszimptóta szükséges a létezését a határértékek (2) és (3). Ha legalább egyikük nem létezik, akkor a lejtőn a asymptote ott. Határértékek (2) és (3) találhatók külön-külön, és mivel a határértékeket eltérő lehet (függvény két különböző asymptote).

Példa 4. Keresse meg a lejtőn a aszimptotáját a grafikonon.

Határozat. A képlet szerint (2) találunk.

Most azt látjuk. Kapjuk egyenlet ferde aszimptotákkal.

5. példa Find aszimptotájának a görbe.

Határozat. Függőleges és vízszintes aszimptotái ott, mióta. Keresünk Tilt:

.

Így, a görbe aszimptotákkal rendelkezik.

6. példa Find aszimptotájának a görbe.

Határozat. Mióta majd a vonalak függőleges aszimptotákkal. Azóta - vízszintes asymptote. Nézzük tisztázni azt a kérdést, hogy létezik a lejtőn a aszimptóta: ezért a görbe meredeksége aszimptóta nem (megjelenés nincs értelme, mivel a horizontális aszimptóta már talált).

Az önálló munkavégzésre.

1. A asymptote meghatározás azt bizonyítják, hogy a vonal egy aszimptótát a görbe.

2. Keresse meg a aszimptotáját az alábbi görbék: