A műveletek egy részét a hálózat menetrendek
A projekt bemutatása a hálózaton keresztül lehet tenni más módon. Mi képviseli a tetejét nem események és műveletek; ív azonos felhasználásra, hogy képviselje a sorrendet, amelyben a műveletek Oij és adott-e már követni, hogy beállíthatja az időkeret kezdete között, és az elején Oij adott-. Ezt a nézetet az úgynevezett „munka”, amit mi hívtuk művelet és „kapcsolat” - egy ív, amely tulajdonítják, mint lehetséges. Ehhez figyelembe a 2.2 ábrát.
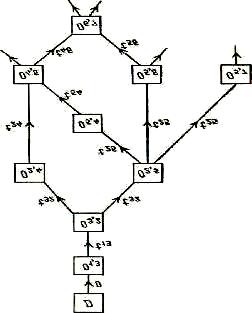
2.2 ábra - Hálózati modell, beleértve a határidők
Ahhoz, hogy teljes mértékben megmagyarázni az átmenet az egyik reprezentáció a másikra, hogy egy másik példa - az átmenet a 2.3 ábra a 2.5 ábra.
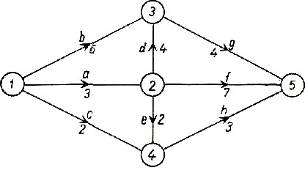
2.3 ábra - A hálózat kezdeti modell
Amint azt a 2.4 ábra és a 2.5, tette hozzá két művet a D és F, amelyek a kezdete és vége a projekt. Figyelembe véve, 2.5 ábra, azt látjuk, hogy a munkát a G után kerül munkáját b és d közötti G és B kapcsolat van: g csak akkor kezdődhet, amikor a pass 6 időegységekben kezdete után b; közötti g és d kapcsolat van: g csak akkor kezdődhet, amikor a pass 4 időegységekben kezdete után d. Másfelől, a művelet d, f, és az e kezdődhet csak menetben 3 egység után az idő kezdete. Mindkét ábrázolások vannak előnyei és hátrányai. Általában választani egyik vagy másik ábrázolás jellegétől függően a feladat, amelyre a projekt összeállítani. Megjegyzendő azonban, hogy a fogalom „kommunikációs művelet” lehetővé teszi, hogy belépjen egy új kommunikációs projekt, vagy a sorrend megváltoztatása közötti kapcsolatok a munkálatok, hozzátéve ívek nélkül hálózat átalakítása egészére.
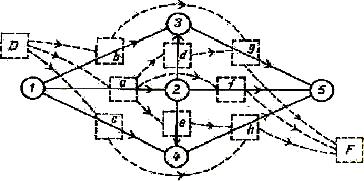
2.4 ábra - Hálózati modell további műveleteket
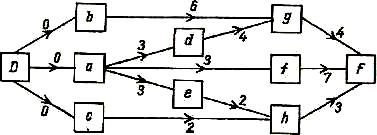
2.5 ábra - A végső hálózati modell
Most néhány példát a különböző helyzetek során esetlegesen felmerülő megfogalmazásában a hálózaton.
A műveletek egy részét a hálózat menetrendek
Párhuzamos működés. Tegyük fel, hogy két esemény között Ei és Ej két különböző művelet b és c, a műtétet követő egy.
Bemutatjuk majd egy fiktív esemény Ej és további fiktív ügyletek között x Ei és Ej. Abban az esetben, ha három, négy, és így tovább. E. Párhuzamos működés, nem ugyanaz, bevezetésével az egyes esemény és egy további fiktív dummy működését, amint azt a 2.6 ábra.
2.6 ábra - Párhuzamos működés egy hálózati modell
Függő és független működését. Tekintsük ábrán 2.7 tranzakciók és d, követve a és b. Tegyük fel most, hogy a következő egy, és b, d, de csak követi a B, és nem köteles követni a. Ebben az esetben ez már nem lehetséges, hogy a hálózat és meg kell adnia E'3 esemény és egy hamis művelet x, amint azt a 2.8 ábra.
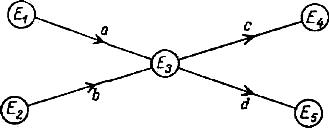
2.7 ábra - függő műveletek
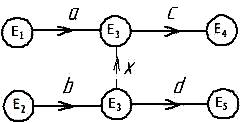
2.8 ábra - Független működés
2.3 korlátozásoktól függően. Kritikus út. tartalék idő
Tegyük fel, hogy néhány művelet csak akkor kezdődhet bekövetkeztével egy bizonyos ponton, azaz. E. után egy bizonyos idő után az események E1 kapott a kezdeti [13, p. 124]. Ezt a korlátozást a kifejezett bevezetése dummy műveletek közötti z E1 és esemény Ei, ahol tekinthető művelet kezdődik. Ez látható a 2.9 ábra.
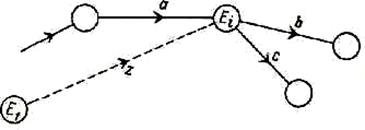
2.9 ábra - Limit egy fiktív ügyleteket
Ábra 2.10 és 2.11 utalnak az esetben, ha szükség van, hogy két fiktív műveleteinek x és z: műveletet követően a jól el kell halasztani az időt z.
2.10 ábra - korlátozása két fiktív műveletek
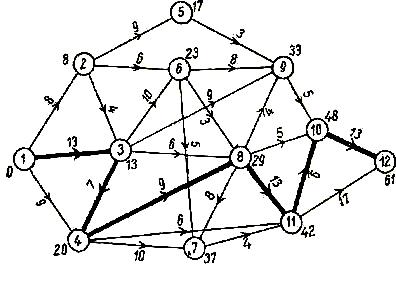
Ábra 2.11 - Kritikus Path
Sok probléma van néhány „körülmények kialakulásának késleltetésére: a művelet”; ezek például a szállítási idő az anyagok, az éghajlati viszonyok és így tovább. n. Ahogy meglátjuk, ezek a speciális körülmények könnyen beépíthetők a hálózatba.
Annak érdekében, hogy figyelembe tudják venni az ilyen korlátozások és bemutatni őket a hálózathoz, fogalmazza meg másképp: „Ahhoz, hogy valami munkát j lehetne kezdeményezni, az szükséges, hogy az idő kezdete óta eltelt egy másik mű j, nem volt kevesebb (- tij) »; ez vezet a normális kapcsolatokat, de a negatív időtartamú (megfelel az ív hossza negatív lesz), ez nem feltétlenül jelenti azt, növekvő bonyolultsága a probléma megoldásának.
Most az élet a hitel befejezése minden munka, és ez vezet minket, hogy a fő tartalma ez a munka - a módszer a kritikus út.
befejezését összetett műveletek időben. Kritikus út. Ha a projekt hálózat épül, a következő kérdés: mi van itt az ideje, hogy befejezték az egész komplexum műveletet, azaz, mi az a projekt időtartama ... Ezúttal nem lehet kevesebb, mint a műtét időtartama mentén vett „legkedvezőtlenebb módon” E1 En t. E. mentén egy ilyen utat két pont között, amely a maximális mennyiségű időigényes művelet. Egy ilyen út (lehet, hogy több) az úgynevezett „kritikus út”.
Figyelembe időtartamával műveket érdemes egy hosszadalmas művelet mentén „legkedvezőtlenebb út E1 En”, mi így lehetőséget ad a tényleges végrehajtása során tervezett ügylet, figyelembe véve a hosszú távú [13, p. 136].
Az egyik matematikai készítmények, amely lehetővé teszi, hogy megoldja ezt a problémát az alábbiakban ismertetjük.
Kezdve az események E1, ami hozzá a támadó 0, úgy véljük, minden csúcsából az ív hálózat, amely magában foglalja; minden egyes ilyen ívek hozzá a megfelelő idő műveletet, amely a csatolt egy ív, az idő előfordulási, megfelelő az elején az ív; összehasonlítjuk az eredményeket, és kiválasztja belőlük a legtöbbet, úgy vélik, a legjobb tulajdonság.
Tekintsük ábra 2.11. Az E2 magában csak egy ív (1,2). Mivel már 0 E1, E2, hogy megkapjuk a 0 + 8 = 8. Az E3 tartalmaz két ív (2,3) és (1,3); összehasonlítjuk a 8 + 4 = 12 0 + 13 = 13, E3 attribútum értéke 13; ez azt jelenti, hogy a támadó E3 esemény nem várható, mielőtt 13. E4 áll két ív (3,4) és (1,4); összehasonlítjuk a 13 + 7 = 20 0 + 9 = 9, E4 attribútum értéke 20. Az attribútum értéke E5 E6 17. tartalmaz két ív (2,6) és (3,6); összehasonlítjuk 8+ 6 = 14 a 13 + 10 = 23, attribútum érték E6 E8 23. A három ívek (6,8), (3,8) és (4,8); összehasonlítjuk a 23 + 3 = 26, 6 = 13 + 19 és 20 + 9 = 29, E8 attribútum értéke 29. Ez addig folytatódik, amíg az esemény En, amely végleg attribútum értéke 61.
Ez a szám az a projekt végrehajtásához, kezdve a nulla pont. A megfelelő útvonalon ezúttal a 61 egységben, ez könnyen kap vissza lépésről lépésre vissza E12 az E1; ez lesz a kritikus út. A 19. ábra, az jelölve van egy vastag vonal.