Célkitűzések a geometriai meghatározása valószínűsége
Probléma 1: A téglalap 5 cm 2 * 4 írt kör sugara 1,5 cm Mi a valószínűsége, hogy az a pont véletlenszerűen meghatározott egy téglalapot, majd a körön belül.?
Megoldás: meghatározás szerint a geometriai valószínűség kívánt valószínűség az területének aránya a kör (amelyben a pontban kell esnie) a terület egy téglalap (amelyben egy pont elhelyezett), azaz Válasz: 0353
Adachi 2: Mi az esélye a találkozó egy barátja, ha megállapodtak abban, hogy megfeleljen egy adott helyen, 12,00-13,00 óra, és várnak egymásra 5 percig?
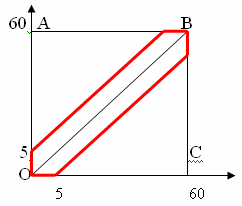
Megoldás: Jelöljük X és az érkezési idő, 0 ≤ x, y ≤ 60 (perc). Egy derékszögű koordináta-rendszer megfelel ennek a feltételnek elhelyezkedő pontok a szögletes OABC. Barátok találkozik, ha nem több, mint 5 perc elmúlik között pillanatában érkezés, azaz y - x <5, y>0, x - y <5, x> y. Ezek az egyenlőtlenségek megfelelnek a ponton, amely G, vázolt piros.
Problémák a Bernoulli formula
1. feladat: Az n akkumulátor tárolás k évben sikerül. M véletlenszerűen kiválasztott elemeket. Határozzuk meg annak a valószínűsége, hogy egy részük l javítható. n = 100, K = 7, m = 5, l = 3.
Megoldás: Van Bernoulli rendszer paraméterekkel p = 7/100 = 0,07 (a valószínűsége, hogy az akkumulátor nem károsodik), n = 5 (a vizsgálatok száma), k = 5-3 = 2 (a szám a „siker”, hibás akkumulátor ). Fogjuk használni a Bernoulli-egyenlet (a valószínűsége, hogy n vizsgálatokban az esemény fordul elő k-szor). Kapunk a válasz: 0,0394.
2. feladat: Olyan eszköz, amely öt függetlenül működő elemek szerepelnek a időben T. A meghibásodási valószínűség az egyes őket ebben az időben 0,2. Annak a valószínűsége, hogy megtagadja: a) a három elem; b) nem kevesebb, mint négy tagja; c) legalább egy elem.
Megoldás: Van Bernoulli rendszer paraméterekkel p = 0,2 (a valószínűsége, hogy egy elem sikertelen), n = 5 (a vizsgálatok száma, vagyis az elemek száma), K (száma „siker”, nem sikerült elemek). Fogjuk használni a Bernoulli-egyenlet (a valószínűsége, hogy n elem meghibásodása esetén a k elemek): Szerezzen be egy) - annak a valószínűsége, hogy pontosan három elem adja fel öt. b) - a valószínűsége, hogy a hulladék legalább négy az öt elem (azaz, vagy négy, vagy öt). c) - a valószínűsége, hogy a hulladék legalább egy elem (talált keresztül a valószínűsége az ellenkező esetben - senki elem meghibásodik). Válasz: 0,0512; 0,00672; 0,67232.
3. feladat: Hogyan kell játszani a sakk a nyerési valószínűsége egy batch 1/3 a legvalószínűbb nyer egyenlő 5?
Megoldás: A legvalószínűbb szám K arány meghatározása a képlet Itt p = 1/3 (nyerési valószínűsége), q = 2/3 (veszteség valószínűség), n - a száma ismeretlen felek. Behelyettesítve ezeket az értékeket, kapjuk Azt látjuk, hogy n = 15, 16 vagy 17. A: 15, 16, 17.
Kihívások a tételek az összeadás és a szorzás valószínűségek
1. feladat: kiadói újság expedíció küldött három postahivatalokban. Annak a valószínűsége, időben történő szállítás az újságok, hogy az első rekesz egyenlő 0,95, a második - 0,9, a harmadik - 0,8. Annak a valószínűsége, a következő események: a) csak az egyik ága megkapja az újságot időben; b) legalább egy rekeszt kap papírokat végén.
Megoldás: Bemutatjuk az eseményeket A1 = (újságok szállítani egy időben, hogy az első rekeszben), A2 = (újságok szállított egy időben a második rekesz), A3 = (újságok szállított egy időben a harmadik rekeszben), azzal a feltétellel, P (A1) = 0,95; P (A2) = 0,9; P (A3) = 0,8. Keressük az esemény valószínűsége X = (csak egy rekeszt kap az újság abban az időben). Esemény X történik, ha vagy újságot szállított egy időben az egyik rekeszben, és a szállított a rossz időben a 2. és a 3. vagy újságok szállított azonnal 2 rész, és szállított a rossz idő, az 1 és 3, vagy újságok szállított azonnal 3 rekesszel, és nem nyilvánított alkalommal a 2. és 1. tehát az események A1, A2, A3 - független, a tételek az összeadás és a szorzás megkapjuk Keressünk a valószínűsége az esemény Y = (legalább egy rekeszt kap az újság végén). Bemutatjuk az ellenkező event = (minden ága megkapja az újságot az idő). Annak a valószínűsége, ez az esemény, akkor a valószínűsége esemény Y: A: 0,032; 0,316.
2. feladat: két, egymástól függetlenül működő jelző készlet jelző baleset. Annak valószínűsége, hogy a kapcsoló aktiválja egy balesetben, 0.95 az első jelző eszközt, és 0,9 a második. Annak a valószínűsége, hogy csak egy kapcsoló aktiválja a baleset.
Megoldás: Bemutatjuk független események: A1 = (az első kapcsoló aktiválja vészhelyzetben); A2 = (második kapcsoló aktiválja baleset); azzal a feltétellel, feladatok P (A1) = 0,95, P (A2) = 0,9. Bemutatjuk az esemény X = (csak egy kapcsoló aktiválja a baleset). Ez az esemény történik, ha egy baleset váltott az első kapcsoló és a második nem fog működni, vagy ha a baleset kiváltó második kapcsoló és az első nem működik, vagyis akkor a valószínűsége esemény X a tételek az összeadás és a szorzás valószínűségek Válasz: 0,14.
3. feladat: Annak a valószínűsége, legalább egy ütő a cél négy lövések egyenlő 0,9984. Annak a valószínűsége, ütő a cél egy lövés.
Megoldás: Legyen - annak a valószínűsége, ütő a cél egy lövés. Bemutatjuk az esetben, ha az X = és az ellentétes event =. esemény valószínűsége, akkor az esemény valószínűsége X. A hipotézis, ez a valószínűség 0,9984, amely hozamok az egyenletet: 0,8.