Határozza elmozdulás vektort és a nyúlvány) az x-tengelyen - prezentáció 99.061-7
<<Проекция вектора перемещения равна разности координат конца и начала
Két hajó a folyón ellentétes irányba, és megfelel a >>
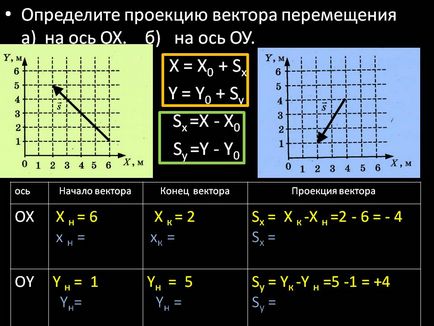
Határozza meg a vetületét elmozdulásvektorból a) OX. b) az y-tengelyen. X = X0 + Sx Y = Y0 + Sy Sx = X - X0 Sy = Y - Y0. Oh. X n = x n = 6. X k = xk = 2. Sx = X rX n = 2-6 = - 4 Sx =. Oy. N = 1 Y = yn. Yn = yn = 5. Sy = yk -Y n = 5 -1 = +4 sy =. Axis. kezdve a Vector. Vége a vektor. A vetítés a vektor.
7. dia bemutatás „meghatározása a koordináta vektor”
Méret: 720 x 540 pixel formátumban. jpg. A dia letöltéséhez használata az osztályteremben, kattintson jobb egérgombbal, kép, és kattintson a „Kép mentése más néven. ”. Töltse le a teljes prezentáció „definiálása koordináta vektora.ppt” lehet zip-archívum mérete 2806 KB.
Kapcsolódó bemutatása
"Moving Grade 9" - Mozgás: hajlított egyenes. Mozgás -. Bonyolult feladat! Röppálya - Lat. köv. - mozgás. Röppálya -. A hossza az út. Way -. - Az irányított szegmens összekötő a kezdeti és a végső helyzetét a test. Merry feladat: Hosszúság 400 futópad stadion. Mik voltak a nyomok az úton?
„A bezárt szög vektorok” - közötti szög a vektorok. A skaláris szorzata vektorok. Keresse meg a bezárt szög a és b vektorok? A tulajdonságok a belső terméket? Hogyan lehet megtalálni a koordinátákat a középpont? Számoljuk ki a koszinusza a szög a sorok között. Mekkora szöget zár be a két egyenes között BD és CD1. Vizuális bemutató a tutorial. A bezárt szög AB és CD egyenesek.
„Skalár termék” - Számítsuk skalár szorzata vektorok: a) és b) és c), valamint. Find skalár szorzata a vektorok (1, 2) és a (2, -1). Skaláris termék és jelöljük. A skaláris szorzata vektorok. Milyen értéken a vektor merőleges vektor t. ha (2, -1), (4, 3). Keresse szög a háromszög csúcsot.
"Vektor Grade 9" - Polygon szabály. A paralelogramma. Hosszúság (egység) vektor. Kollineáris vektorok. Ezenkívül a vektorok. Kollineáris vektorok. háromszög szabályt. Vektor. hogy a vektorok egyenlő?
„Vektoros problémák megoldását” - kifejező vektorok AM, DA, CA, MB, CD keresztül vektor és b vektor. BE. EC = 3. 1. K - a középső DC. Sze PD = 2. 3; AK. KD = 1. 2. kifejezésére CK vektorok keresztül RK a és b vektorok. Express vektorok AE, AK, KE és az a és b vektorok. A vektorok használata, hogy megoldja a problémákat (1. rész). № 1 nap vektorok kifejezni, CD, AC, OC, OA az a és b vektorok.