feladat №61
Feltételezések alapján a klasszikus lineáris modell szerint:
- ahol több együttható meghatározása és magyarázza a jelentését;
- megtalálni az egyenlet YX = a0 + a1 x1 + x2 a2 többszörös regresszió YX az x1. x2. és értékelje a jelentősége ennek egyenlet és együtthatók szinten a = 0,05;
- összehasonlítani külön befolyásolja a függő változó az egyes magyarázó változók standardizált regressziós együtthatók és együtthatók rugalmassági;
- találni 95% -os megbízhatósági intervallum a regressziós együtthatók és a konfidencia intervallumok az átlagos egyedi paramétereket és az értékeket a költsége 1 m az öntés boltok, ahol az öntési 1 termelésben dolgozó munkások 11 m, és a házasság a casting - 7%.
- Paraméterbecslés többszörös lineáris regresszió
Méretezése többszörös lineáris regressziós végezzük mátrix formában:
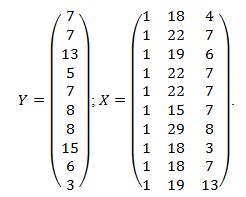
Azt találjuk, egymás után a mátrix és a vektor (X T X) -1. Van X T Y

Most kiszámoljuk a fordított mátrix (X T X) -1:
Továbbra is szaporodnak a mátrix (X T X) -1, és a vektor X T Y:
a regressziós egyenlet:
Az így kapott egyenlet azt jelenti, hogy a termelés növelése egy működési költség 1 tonna tonna öntvény csökken átlagosan 0003 ezer. Dörzsöljük. A növekedést a házasság 1% költsége 1 tonna öntvény esik átlagosan 0,955 ezer. Rub.
Nyilvánvaló, hogy a faktor x2 sokkal nagyobb hatást gyakorol a hatékony jele, mint x1 tényező.
- Kiszámítása több determinációs együttható
A többszörös determinációs együttható alábbi képlettel számítottuk ki:
Kiegészítő számítások megbecsülni a determinációs együttható a táblázatban látható.
Kiszámítása több determinációs együttható
A többszörös determinációs együttható értéke:
A kapott érték a meghatározás együtthatója azt jelenti, hogy 50% a költség egy tonna öntés kifejtett variációkkal épített regressziós egyenlet, és a 50% - egyéb tényezők következtében.
- Értékelését a következő egyenlet és együtthatók
Értékelését a következő egyenlet egészének útján F-Fisher kritérium:
ahol: n - a megfigyelések száma;
m - a paraméterek száma a x változó.
F-Fisher kritérium:
Táblázatból vett érték F-teszt szignifikancia szintje 0,05 és száma a szabadsági fokok k1 = m = 2, és k2 = n -m -1 = 7 egyenlő 4737.
Mivel a kiszámított értéket az F-próba az alábbi táblázatot, a null hipotézist fogadták, hogy a meghatározás együttható nulla, azaz a összeállított regressziós egyenlet statisztikailag nem szignifikáns.
Mi található a pontbecsléseket az összes rendelkezésre álló változók:

Mi található a standardizált regressziós együtthatók és rugalmasságát az egyes magyarázó változók. Van:
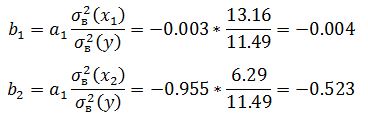
Mivel standardizált regressziós együttható a második tényező nagyobb, van egy nagyobb hatással szimptóma. Standardizált regressziós együttható változó x1 közel nulla, ami azt jelenti, hogy a befolyásoló tényezők a fröccsöntő költség lényegtelen.
Kiszámítjuk a rugalmasság:
Ez azt jelenti, hogy amikor a faktor x1 1% pontszámot jel változás 0,008% az ellenkező irányba. Ha megváltoztatja a tényező x2 1% -os eredmény jel változás 0,834%.
Így a befolyásoló tényezők „Százalék házasság” sokkal fontosabb, mint a változó a „Generation casting per munkás.”
- Meghatározása konfidenciaintervallumai regressziós együtthatók
A lényeg becslése hibavariancia:
A maradék szórás:
Megbízhatósági intervallumok megbízhatósági szinten 0,95 regressziós együtthatók az űrlap
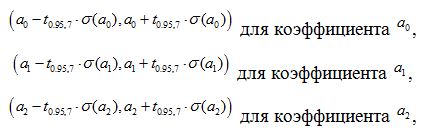
elemek állt a diagonális mátrix (X T X) -1. Mátrix (X T X) -1 korábban találtak kifejezetten így
Táblázatból vett érték t-próba a számát szabadsági fok és 7 a szignifikancia szint 0,05 egyenlő 2,365. Konfidenciaintervallumai regressziós együtthatók megegyeznek:
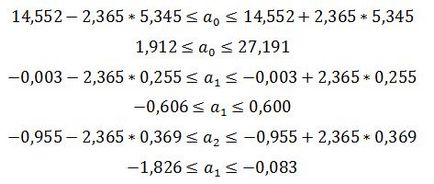
A számítások azt mutatják, hogy a megbízhatósági intervallum paraméter a1 tartalmaz 0; 95% regressziós koefficiens a1 nulla. Ez azt jelenti, hogy a változó x1 nem befolyásolja a termelési tényező.
Mi a becsült érték a költség egy tonna öntés, ha a kimeneti dolgozóra jutó 11 m, és a selejt arány - 7%:
A képlet a megbízhatósági intervallum átlagos értékekhez formában van
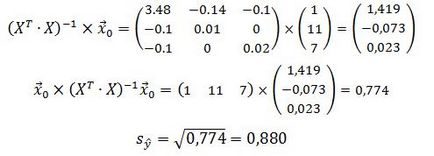
A megbízhatósági intervallum középértéke a tényleges jellemzője:
Y ε (7834 - 2,365 * 0,880; 7834 + 2,365 * 0,880) = (5754; 9915)
Következtetés. egy 95% -os valószínűséggel az átlagos költsége tonnánkénti öntés a készítményt per munkás 11 m, és a selejt-arány 7% közötti tartományban van a 5,754-9,915 ezer. dörzsölje.
Az egyes értékeinek változó Y megfelelő konfidencia intervallum adja meg:
Y ε (7834 - 2,365 * 1,332; 7834 + 2,365 * 1,332) = (4,685; 10,984)
Következtetés. egyes jellemző értéket a készítmény 11 m és a 7% -os szinten házasság egy 95% -os valószínűséggel van a tartományban 4685 és 10.984. dörzsölje.