Hogyan lehet megtanulni, hogy megoldja a mátrix
Rejtélyes első mátrix valójában nem olyan nehéz. Úgy találják, széles gyakorlati alkalmazása közgazdasági és számviteli. Úgy néz ki, mint egy mátrixot tartalmazó táblázat számok minden sorban és oszlopban, a funkció, vagy bármely más értéket. Rengeteg féle mátrixok.
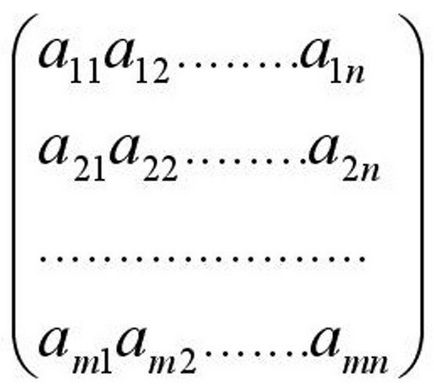
oktatás
Annak érdekében, hogy megtanulják, hogyan kell megoldani a mátrix, megismerkednek az alapvető fogalmakat. A meghatározó eleme a mátrix átlós - fő és másodlagos. Otthon kezdődik az elem az első sor, első oszlop és addig folytatódik, amíg az elem az utolsó oszlop, utolsó sor (azaz megy balról jobbra). Mellékes ugyanazon átlós kezdődik fordítva az első sorban, de az utolsó oszlop, és kiterjeszti a cella koordinátáit az első oszlop és az utolsó sor (megy jobbról balra).
Annak érdekében, hogy folytassa a következő meghatározásokat és algebrai műveletek mátrixokkal, megvizsgálja típusú mátrixok. A legegyszerűbb közülük - egy négyzet, átültetés, egység, nulla és vissza. Egy négyzetes mátrix azonos számú sorok és oszlopok. Az átültetett mátrix, nevezzük B nyerik az A mátrix helyettesítésével oszlopok sorokra. Az identitás mátrix minden elemét a fő átló - egység, míg mások - nulla. És még a nulla átlós elemek nulla. Inverz -, hogy amikor megszorozva az eredeti mátrix, amely jön egy elme.
Továbbá, a mátrix lehet szimmetrikus fő tengelye vagy járulékos. Azaz, az elem, amelynek a koordinátái a (1-2), ahol 1 - a sor számát, és a 2 - oszlop egy (2-1). A (3-1) = A (1-3) és így tovább. A mátrixokat megállapodtak - azok, ahol az oszlopok számát egyenlő a sorok számát egy másik (például mátrix lehet szorozni).
A fő, hogy milyen műveleteket végezhet a mátrixok - ez összeadás, szorzás és megtalálja a meghatározó. Ha a mátrix az azonos méretű, azaz ugyanolyan számú sort és oszlopot, akkor lehet hajtani. Fold szükséges elemeket ugyanazon a pozíciókat a mátrixok, azaz egy (m-n) a hajtás a (m-n), ahol m és n - a megfelelő sor és oszlop koordinátái. Azáltal, hogy a mátrix műveletek fő szabály a szokásos aritmetikai kívül - a változás összeg nem változik. Így, ha ahelyett, hogy egy egyszerű sejt van a mátrixban és a kifejeződése A + B, ez lehet süllyeszteni a másik elemhez szabályok arányos mátrix a + (b + c) = (a + b) + c.
Szorzás mátrixok lehet hangolni, a fentiekben meghatározott. Ez ad egy mátrixot, ahol minden egyes elem - az összege páros szorzatát elem sorai A mátrix és a mátrix B. Ha az oszlop megszorozzuk nagyon fontos eljárás. m * n nem egyenlő n * m.
Ez is az egyik fő intézkedés - megtalálni a meghatározója a mátrix. Más néven meghatározó jelölnek: det. Ez az érték határozza meg a modul, amely soha nem negatív. A legegyszerűbb módja, hogy megtalálják a meghatározója a téren, egy 2x2 mátrix. Ehhez szorozza meg a fő átlós elemek és le kell vonnia a szorzatát másodlagos átlós elemek.