Funkcionális szekvenciák és sorozatok
14. Funkcionális szekvenciák és sorozatok
Eddig úgy csak a numerikus szekvenciák és numerikus sorozat. Most tanulmányozni fogjuk a sorozat, amelynek elemei - a funkció, valamint a sorozat, amelynek feltételei a függvények.
14.1 pontonkénti és egyenletes konvergenciája
Tekintsük a sorozat funkciók
f1 (x). f2 (x). f3 (x). halmazán megadott EIR. Tegyen meg minden AIE. Behelyettesítve x a. Kapunk egy számsor n (a)>. Meg lehet közelíteni, vagy eltérhetnek. A számok halmaza a. amelyet történő helyettesítésével kapott számszerű sorrendben konvergálnak, az úgynevezett dómén szekvencia konvergencia n (x)>. Mi lesz halmaza a D betű:
Minden egyes támogatási véges határ, ami mi jelöljük f (a):
.
Van használt funkcionális rekord f (a), amikor hivatkozva a számot, hogy hangsúlyozzák, hogy ez a határ függ. azaz függvénye a. Használhatja a jobban ismert jelölést a változó:
, nem megfeledkezve, hogy f (x) van meghatározva csak a beállított D. használt felvétel ikonra nélkül lim. . Ilyen konvergencia a szekvencia N (x)>, hogy az f (x) pontonkénti. Adunk meghatározását pontszerű konvergencia nyelvén «e -d»:
.
Most definiáljuk egyenletes konvergencia, amely jelöljük az alábbiak szerint: (olvasni „szekvencia fn (x) konvergál egyenletesen a beállított D egy f (x)”). definíció szerint,
.
Első pillantásra egy kis különbség a definíciók, de elengedhetetlen. Az első meghatározás szükséges, hogy minden szám ott rejtette n0 egy bizonyos tulajdonság. Különböző olyan x szám különböző lehet. A második meghatározás - sokkal követelmény: az azonos számú n0 alkalmas legyen bármilyen HID. Így egyértelmű, hogy a konvergencia egyenletes következőképpen pontonkénti:
.
Fordított - rossz, lásd az alábbi 1. példa ..
Adunk egy geometriai illusztrációja fogalmának egyenletes konvergencia. Az a követelmény meghatározása:
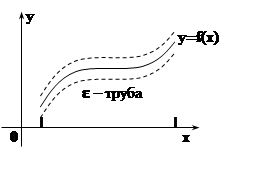
azt jelenti, hogy, kezdve egy bizonyos számú grafikus Fn (x) nem különböznek lényegesen a grafikon f (x) a teljes készlet D. fekszenek «e -trube” a grafikon az f (x). Így
grafika fn (x) tartozik a «e- cső” képe f (x).
Example1. Tekintsük a sorozat funkciók
Feltesszük xid = [0, 1]. Minden pont a beállított sorrendben konvergál: