Elméleti végtelen tizedes jegyek - a fogalom egy valós szám
A tényleges száma is meg van adva, mint egy végtelen tizedes, majd a kifejezés formájában. ahol az egyik szimbólumok vagy. Azt az úgynevezett jele száma, - nem negatív egész szám, - egy sorozata decimális számjegy, vagyis több olyan numerikus elemek.
Végtelen tizedes értelmezi a szám, ami a számegyenesen között fekszik racionális pontok formájában
Összehasonlítása valós számok formájában végtelen tizedes jegyre történik apránként. Például tegyük fel, hogy adott két nem-negatív szám
Ha. akkor; Ha ezt. Egyenlőség esetén összehasonlítás továbblép a következő mentesítési. És így tovább. Ha. Ez megfelel az első számjegy után véges számú lépésben. úgy, hogy. Ha. akkor; Ha ezt.
Ha azonban összehasonlítjuk a végtelen tizedes kérjük, vegye figyelembe, hogy a számot. Ebben az esetben, ha a felvétel az egyik számot, hogy összehasonlítjuk az elején egy bizonyos kategóriába, egy ismétlődő tizedes, amely áll egy olyan időszakban, 9, akkor ki kell cserélni egy egyenértékű bejegyzést nulla időszakban.
Aritmetikai műveleteket végtelen tizedes frakciókat meghatározása a folytonos meghosszabbítását [14] megfelelő műveleteket racionális számokat. Például, az összeg a valós számok nevezzük valós szám. kielégíti a következő feltételt:
Hasonló módon határozzuk meg a szorzás művelet egy sor végtelen tizedes frakciók.
A legtöbb esetben a pontos hányados decimális formában nem nyerhető, nem számít, milyen messze folytatódott részlege.
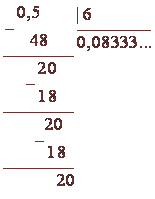
Frakció alakítjuk decimális periodikus tiszta, mivel a 27 nem osztható 2 vagy 5. frakció alakítjuk vegyes szakaszos, hiszen 12 osztva 2.
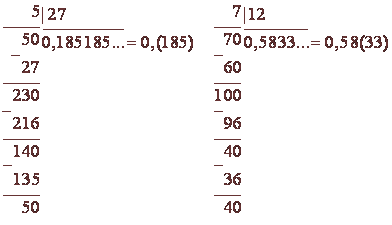
Bizonyítsuk be, hogy végtelen tizedes ,1234567891011121314. (Miután a tizedes pont van írva egymás természetes szám egymást követő sorrendben) egy irracionális szám.
Mint ismeretes, a racionális számok kifejezve tizedesjegyben, amelyek kezdődő időszak egy bizonyos jel. Ennek alapján elegendő annak bizonyítására, hogy a frakció nem periodikus, vagy egy jel. Tegyük fel, hogy nem ez a helyzet, és egy olyan szekvenciát T, amely n számjegyek, az az időszak, a frakció, kezdve a m-edik tizedesjegy pontossággal. Ebben az esetben, hogy a nem nulla, így a T--számjegysor egy nem nulla számjegy között találhatók a számok után a m-edik karakter. Ez azt jelenti, hogy, kezdve a m-edik decimális hely között bármely n egymást követő számjegy egy nem nulla számjegy. De ebben a tizedes törtet kell jelen lennie decimális szám 100. Entry 0 = 10 k. ahol k> m és k> n. Magától értetődik, hogy a helyes bejegyzést Meet m-edik számjegy, és tartalmaz több, mint N egymást követő nullák. Így van egy ellentmondás, amely befejezi a bizonyíték.
Adott egy végtelen tizedes tört 0, a1 a2. Bizonyítsuk be, hogy a számjegyek a tízes számrendszerben lehet összeállítani, hogy a frakciót egy racionális szám.
Töredék fejezi racionális számok akkor és csak akkor, ha az időszakos, kezdve egy bizonyos határt. Számok 0-9 vannak osztva két osztályba tartozhatnak: az első osztályú közé tartoznak azok a számok, amelyek megtalálhatók a kezdeti frakciókat véges számú alkalommal, a második osztály - azok, amelyek előfordulnak a kezdeti frakciókat végtelen számú alkalommal. Először felírni periodikus frakciót, amely beszerezhető a kezdeti permutációját számok. Kezdetben, miután a nullpont és írjon bármilyen sorrendben a számokat az első osztályban - minden ahányszor kiderül, a rekord az eredeti frakció. Rögzített számok az első osztályú lesz előzi meg a tört része a tizedes. Ezután írd le egy bizonyos sorrendben, ha a szám a második osztályban. Az így kapott kombinációt nevezzük időszakban, és ismételje meg a végtelen számú alkalommal. Ily módon írtunk az előírt időszakos frakció kifejező racionális szám.
Bizonyítsuk be, hogy minden végtelen tizedes tört van egy sorozat a decimális számjegy tetszőleges hosszúságú, ami a bővítés a frakció talált végtelen számú alkalommal.
Legyen m - önkényesen természetes szám. Azt ossza ez a végtelen tizedes tört be szegmensek m számjegy egyes. Ezek a szegmensek lesznek végtelen. Másrészt, a különböző rendszerek, amelyek m szám, csak 10 m. t. e. véges. Ebből következik, hogy legalább az egyik ilyen rendszereket kell ismételni itt végtelen sokszor.
Megjegyzés. Az irracionális számok # 118, 2, p vagy f még azt sem tudja, mi az ábra ismétlődik végtelen sokszor képviseljék végtelen tizedes tört, de minden ezen számok könnyű bizonyítani, legalább két különböző ilyen számokat.
Ellenőrizze a hosszú divízió
Így az összes racionális számok között szerepel a végtelen tizedes jegyek periodikus tizedes.
Valós számok nevezzük végtelen tizedes jegyek egy plusz vagy mínusz, abban az esetben a frakciók a periodicitás egy valós számot hívják racionális, különben - irracionális.
A szám a = 0,1010010001. mint egy végtelen nem periodikus tizedes irracionális szám.
Ez viszonylag könnyű meghatározni a kapcsolat és a rend az egyenlőség ( „nagyobb”) Legyen a = 0. 1. 2. b = 0. 1. 2.
valós számok. Úgy véljük őket megegyezik, ha ugyanaz az előjele, és k = 0, 1, 2, k = k.
Legyen a, b egy "+" jel. A szám nagyobb, mint a szám b (a b), ha k = 0, 1, 2, hogy i = i i = 1, 2 k - 1 és KK