vékony lencse
Rajzoljunk egy tangenciális síkban a felületek a lencse pontokon M és N. és felhívni ezeket a pontokat görbületi sugarak R1 és R2 a lencse. Ezután Amna gerenda lehet tekinteni, mint egy sugár megtörik a kis prizma megtörőt szög # 1256;. Tekintettel a kicsinysége szögek # 945;, # 946;. # 945; 1 # 946; 1 és a lencse vastagsága tud írni a következő közelítő egyenlet:
Tól AHA1 és BEB1 háromszögek következik, hogy
Figyelembe véve (3.5), megkapjuk
De, képlet szerint (3.4), # 948; = (N - 1) # 1256;. ezért
Ezt az összefüggést nevezzük a lencse formula. A képlet nem tartalmazza a h1 magasság. Ez azt jelenti, hogy a távolság b nem függ a helyét M. azaz Minden sugarak áradó pont gyűlik össze, miután fénytörés más szemmel részei egy ponton A1.
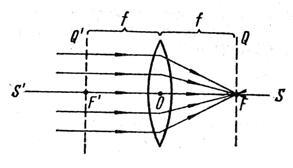
Ehhez kapcsolódik, hogy ha ez a távolság b = OF = f nevezzük gyújtótávolság a lencse:
Ebben a környezetben f ez csak attól függ, törésmutatójú és a görbületi sugarak a lencse. Pont F és F”, ami hazugság mindkét oldalán a lencse egyenlő távolság a gyújtótávolság, az úgynevezett fókusz a lencse. A sík merőleges a gócok a fő optikai tengely, az úgynevezett fokális síkban.
Belátható, hogy a sugarak beeső a lencse párhuzamos a járulékos optikai tengellyel egy ponton után fénytörés N, fekvő fókuszsíkjában (ábra. 3.10).