Miért tudomány geometria - a geometria a prezentáció
A munka lehet használni órák és bemutatók terén „Geometry”
Ez a rész a helyszínen gyűjtött valamennyi oktatási bemutatók a geometria. Kész előadások geometria segítségével a tanárok kevesebb időt töltenek a rajz bonyolult geometriai formák és még dolgozni az osztály, hogy megoldja a problémákat magukat. Geometry bemutatása hasznos lesz a tanároknak és a szülőknek, hogy segítse a gyermekek házi magyarázatot. Akkor töltse le a teljes előadás geometria órákat 6,7,8,9,10,11 osztályban.

Az információ be van ágyazva a diakép.

Mit jelent a geometria. Mit jelent a geometria. A geometria történetében. Hol tanult geometriát? Típusai szögek. Típusai háromszögek. Miért geometria. És ha nem volt geometria. Információforrások.
Geometriában ága a matematika amely tanulmányozza a tulajdonságait a különböző formák (pontok, vonalak, szögek, kétdimenziós és háromdimenziós tárgyak), azok méretét és relatív helyzetét. A könnyebb tanítás geometria vannak osztva sík és a tér geometriája. Geometriában ága a matematika amely tanulmányozza a tulajdonságait a különböző formák (pontok, vonalak, szögek, kétdimenziós és háromdimenziós tárgyak), azok méretét és relatív helyzetét. A könnyebb tanítás geometria vannak osztva sík és a tér geometriája.

Az egyik leghíresebb tanulók volt Thalész, Püthagorasz (kb 570 - .. Kb 500 BC). Sokat utazott, majd telepedett Crotone, Olaszország, ahol megalapította a társadalom szentelt a tanulmány a számtan, zene, geometria és a csillagászat. Püthagorasz és követői bizonyultak számos új tételek mintegy háromszögek, körök és az arányok az egyes háromdimenziós szilárd. Püthagorasz is bebizonyította a híres tétel, hogy az ő nevét viseli ma, amely szerint a terület a tér épül átfogó egy derékszögű háromszög egyenlő az területének összege a négyzetek épül Catete. Középkorban. Bukása után Alexandria, a legtöbb munka az ókori görög matematikusok voltak szétszórva, vagy elveszett. Egyesek, köztük Euclid, arra fordította és tanulmányozta az arabok és indiaiak. Bár ezek az emberek hoztak létre számos kiváló matematikus, melyek közül a legismertebb indiai matematikusok Árjabhata (kb 476 - .. Kb 550) és Bhaskara II (. Ca 1114-1185), mégis a legnagyobb érdeme kell tekinteni megőrzése a geometria a középkorban.

Geometry használják mindenhol. A szó geometria áll rendelkezésre minden nyelven a világ. Ez további bizonyítéka annak szükségességét. angol német geometria Geometrie geometrie francia olasz spanyol geometria Geometria

A mi korunkban, a geometria - a tényleges kutató tudomány minden iskolák, egyetemek és felsőoktatási intézmények. A mi korunkban, a geometria - a tényleges kutató tudomány minden iskolák, egyetemek és felsőoktatási intézmények. Azokban az iskolákban, a gyerekek megtanulják a tárgya a 7. osztálytól. Geometry követeli pridelnyh gondos és alapos felkészülés a leckét. Geometria - a lényeg mindenki életében, így kezeljük azt, hogy fontos állt az első szerelem.

És hogyan kell elképzelni az életet anélkül geometriai formák. És hogyan kell elképzelni az életet anélkül geometriai formák. Most megmutatjuk, azok sokszínűségét. Nélkülük nem tudnánk élni! Azt sem tudja képzelni egy ilyen dolog.
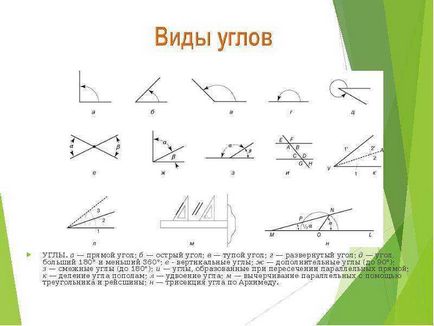
Szögek. és - derékszögben; b - hegyesszög; in - tompaszögben; G - egy egyenes szögben; d - szöge nagyobb, mint 180 °, és kisebb 360 °; e - függőleges szög; W - komplementer szögek (90 °); h - a szomszédos szögek (180 °); és - a szögek által alkotott metszéspontja a párhuzamos vonal; hogy - a szétválás a szög fele; l - megduplázása szög; m - nyomkövetés keresztül párhuzamosan egy T-négyzet és a háromszög; N - szögharmadolás Archimedes. Szögek. és - derékszögben; b - hegyesszög; in - tompaszögben; G - egy egyenes szögben; d - szöge nagyobb, mint 180 °, és kisebb 360 °; e - függőleges szög; W - komplementer szögek (90 °); h - a szomszédos szögek (180 °); és - a szögek által alkotott metszéspontja a párhuzamos vonal; hogy - a szétválás a szög fele; l - megduplázása szög; m - nyomkövetés keresztül párhuzamosan egy T-négyzet és a háromszög; N - szögharmadolás Archimedes.

Triangle. és - a sokoldalú; b - egyenlőszárú; in - egyenlő oldalú; g - téglalap alakú; d - oldalhossza és időközönként egy derékszögű háromszög; e - háromszög szögei; Nos - média H - magassága; és - a szögfelezői szögek; hogy - háromszög, hasadék párhuzamos egyenes egyik fél; l - háromszög boncolt felezővonal egyik sarkok; m - a hasonló háromszögek; N - arányos elválasztó. Triangle. és - a sokoldalú; b - egyenlőszárú; in - egyenlő oldalú; g - téglalap alakú; d - oldalhossza és időközönként egy derékszögű háromszög; e - háromszög szögei; Nos - média H - magassága; és - a szögfelezői szögek; hogy - háromszög, hasadék párhuzamos egyenes egyik fél; l - háromszög boncolt felezővonal egyik sarkok; m - a hasonló háromszögek; N - arányos elválasztó.

Szabályzat emlékeznek jobb, ha szórakozni megfogalmazás. Mindenki tudja, hogy a szabályok emlékeznek jobb, ha szórakozni megfogalmazás. Mindenki tudja, hogy „Szögfelező - Ez patkányok hogy felmászik a sarkok és osztja a szög fele.” CS1 - felezővonal abc1

Tárolni, mint egy képregény rím használta a Pitagorasz-tétel: A tárolásához azonos képregény rím használta a Pitagorasz-tétel: „Pitagorasz-nadrág minden irányban egyenlő!”

Kérdés: Ki a régi matematikusok, megölte egy római katona, büszkén felkiáltott: „Takarodj, ne érintse meg a rajzaim!” Kérdés: Melyik az ókori matematikusok megölt egy római katona kezében, büszkén felkiáltott: „Takarodj, ne érintse meg a rajzaim!” Válaszol: görög tudós - Archimedes. Keresse meg a hiányzó betűt: 1. GMTR ZDCH 2. 3. 4. TRPTS PRPNDKLR Válaszok: 1. geometria 2. A probléma 3. sor 4. merőleges.

Három négyzetes értéke 9. A négy négyzeten egyenlő 16. És mi az a szög a tér? (90 °) három négyzetes értéke 9. A négy négyzeten egyenlő 16. És mi az a szög a tér? (90 °) Mi a háromszög, amelynek két oldala egyenlő? (Isosceles) Vajon a háromszögben két tompaszöge? (Nincs) Mi az az eszköz, szögek mérésére? (Szögmérő) Mi az az összeg, a szögek a háromszög? (180º) néven nevezett vonalak nem metszik a gépen? (Párhuzamos) Hogy hívják paralelogramma, amelynek minden oldala egyenlő, és a szögek egyenes? (Doboz) Mi a műszer hosszúságú? (Vonalzó) Mi az az összeg, szögek? (180º) néven nevezett vonalak metszik egymást derékszögben? (Merőleges)

Sok figyelmetlen hallgatók házi csoda. „Miért van geometria? Általában ő nem jöhet. Miért én házi! Gyerünk! „És sétálni! De nem is hiszem, hasznos számukra az életben! Hogy akkor a jövőben fognak szenvedni! Sok figyelmetlen hallgatók házi csoda. „Miért van geometria? Általában ő nem jöhet. Miért én házi! Gyerünk! „És sétálni! De nem is hiszem, hasznos számukra az életben! Hogy akkor a jövőben fognak szenvedni! Például: Lesz egy diák építő, akkor hozzon létre egy tervet az épület, ha nem érti a geometriai alakzatok, vagy nem találja a skála. És ha például ugyanazt a tanulót, hogy magyarázza, hogy a gyermek a téma, mit mondana? Úgy nézett volna rossz a szemében a gyermek, és adott neki egy rossz példa! Ebből arra lehet következtetni, hogy nem geometria nagyon nehéz élni!

Próbáljuk elképzelni, hogy egy ilyen tudomány geometria nem létezik, ami azt jelenti, hogy a személy nem tudja, hogyan kell hívni a szám! Próbáljuk elképzelni, hogy egy ilyen tudomány geometria nem létezik, ami azt jelenti, hogy a személy nem tudja, hogyan kell hívni a szám! És hogyan kell élni. Itt például, akkor jön a boltba, felejtsd el a termék nevét, hogyan magyarázza, hogy milyen terméket szeretne vásárolni. A legvalószínűbb az eladó nem fogja érteni ezt a magyarázatot, mint a sárga és finom! És hogyan lehet az iskolában, hogyan lehet magyarázni a tábla képező föld labdát.

Hoztam egy bizonyíték arra, hogy a geometria van szükség minden diák! Tegyük fel, hogy használja azt a kis dolgokat, és mindent meg lehet, hogy te és nem bizonyította, hogy a geometria van szükség. De van egy kérdés, ami minden szkeptikus azt hinni, hogy szükség van! Miért az ősi nép, a görög tudós, a középkori tudósok vizsgálták meg? Bevált tulajdonságok és tételei. Miért épp most tanulunk meg, ha nem kell. A válasz egyszerű és elemi - szükség van, mert enélkül nem lennénk. Hoztam egy bizonyíték arra, hogy a geometria van szükség minden diák! Tegyük fel, hogy használja azt a kis dolgokat, és mindent meg lehet, hogy te és nem bizonyította, hogy a geometria van szükség. De van egy kérdés, ami minden szkeptikus azt hinni, hogy szükség van! Miért az ősi nép, a görög tudós, a középkori tudósok vizsgálták meg? Bevált tulajdonságok és tételei. Miért épp most tanulunk meg, ha nem kell. A válasz egyszerű és elemi - szükség van, mert enélkül nem lennénk.

Nagy Szovjet Enciklopédia. Nagy Szovjet Enciklopédia. Saját archívumokat. Encyclopedia "Krugosvet"