Nyereg - matematikai enciklopédia - Enciklopédia és Szótár
- hely típusa pályái autonóm rendszer közönséges differenciálegyenletek 2. sorrendben:
(*)
. G - egyediségét terület, a közelben a szinguláris pont (egyensúlyi helyzet) x0. Ez a típus, jellemzői a következők. Van egy környéken x 0, hogy minden pályái a rendszer, kezdve a pozitív és negatív félig pályagörbét távozik (elhagyni minden kompakt idővel). Az egyetlen kivétel a négy pályák (s e p r t p és s d f c l a). Mert ketten távoznak semitrajectory negatív és pozitív semitrajectory ponttal szomszédos x0. A másik két - éppen ellenkezőleg. Az első kettő az úgynevezett szeparatrixokkal. rezisztens, két második - instabil. Stabil szeparatrixokat egészíti pont x 0 formájában, amely átnyúlik a sima görbe x 0 - stabil gyűjtőcső nyereg. Instabil szeparatrixokat együtt az a pont x 0 formájában sima instabil sokrétű nyereg. S. így nevezett. és az a pont x 0 magát.
Saddle x 0 Ljapunov instabil. A Poincaré-index értéke -1. A rendszer (*) fokozat egy nem zérus mátrix = f „(x 0) többi pontja x 0 jelentése S. abban az esetben, amikor a sajátértékei a mátrix L1 L2 Audovletvoryayut állapotban l1 l, 2 <0 (простое С. рис. 1, где x0 = 0), но может быть С. и в тех случаях, когда или l1 =l2 =0. В любом из этих случаев сепаратрисы С. касаются в точке х 0. направлений, определяемых собственными векторами матрицы А.
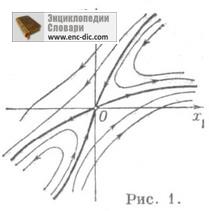
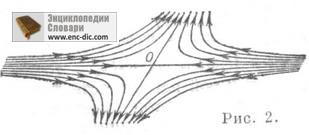
Ha a rendszer (*) jelentése a lineáris (f (x) -A (X-x0), A - állandó mátrix sajátértékei L1 L2), akkor az a pont, x 0 C csak akkor, ha L1 L2 <0. Сепаратрисы седла х 0 в этом случае прямолинейны, а все остальные траектории (отличные от точки х 0 ). суть аффинные образы гипербол вида (рис. 2).
Az „S.” az itt használt minden olyan helyen, a pályák (*) szomszédságában U izolált többi pont x 0, k-beállítani 0 és egy pont x szomszédos csak véges számú pályák, és mindegyikük, egészítik pont x0. Ez vonatkozik egy adott irányban (m-szeparatrixokat C.). S. hívott. és nek- típusú egyensúlyi pontja autonóm rendszer a közönséges differenciálegyenletek rend
Irod cm. cikk értelmében. A szinguláris pont a differenciálegyenlet. AF Andrejev.
Encyclopaedia of Mathematics. - M. szovjet Encyclopedia Vinogradov 1977-1985