Lecke a „primitív”
Rövid leírása a dokumentum:
Az elmúlt órák, van, hogy ismeri a szabályokat megállapító származék függvényében, megismertük a származékok felhasználását funkció tanulmányok a monotónia és a szélsőséges érték; Megtudtuk, hogy megtalálják érintő a függvény grafikonját.
Emlékezzünk számítási szabályainak származékai:
A származék bármilyen szám nulla.
Xxx-származék egyenlő egy.
A származtatott X plusz em ka.
Származó egységeket, osztva X, egyenlő mínusz egy, osztva X a téren.
Derivative gyökere X egyenlő egy osztva négyzetgyök két X.
A származék szinusz koszinusz X X.

A származék koszinusza x mínusz sine X.
X-származék a mértéke HU HU megszorozzuk X ereje mínusz egy en.
Néha van, hogy megoldja a problémákat, inverz, például, hogy állítsa vissza a törvény a mozgás az ismert sebesség.
A matematika, a kölcsönös inverz műveleteket rendelni konkrét neveket.
Például az inverz művelet szorzás - ezt a felosztást.
Működés inverz négyzetgyök kivonása négyszögesítése.
A folyamat a megállapítás a származék egy adott funkciót nevezik differenciálódás és működését, annak inverz, - integráló (folyamat találni ez a származék a funkció).
Ez a funkció a kiálló, mint az őse a származékot ezt a funkciót nevezik primitív.
Definíció: az y egyenlő nagy Aeff X nevezzük primitív függvény y egyenlő kis Aeff X előre meghatározott időközönként X nagy, ha bármely X tartozó ezt az űrt, a következő egyenlőség:
Gap, amely tartozik a X, általában nem jelzett, de értem.
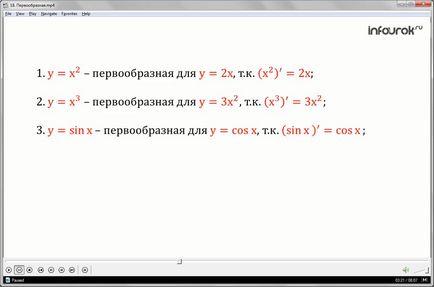
1. Funkciók y egyenlő az X a négyzet egy primitív a funkció y, egyenlő két X, mint bármely olyan X egyenlőség: a származék X négyzetes egyenlő két X.
2. A funkció y, egyenlő X a kocka, egy primitív funkció y egyenlő három X a négyzet alakúak, mint az összes egyenlőség X: X-származék a kocka azonos három X négyzetes.
3.Funktsiya y egyenlő a szinusz X, egy primitív funkció y egyenlő az koszinusza X, mint bármely olyan X egyenlőség: a származékot a szinusz a koszinusza X X
4.EDITING y egyenlő az x négyzetgyöke, egy primitív funkció y egyenlő egy osztva négyzetgyök két X, az intervallumban nullától a végtelenig, mivel bármely x nagyobb, mint nulla, az egyenlőség: a származékot gyökere X egyenlő eggyel, osztva négyzetgyök kettő X.
Ismerve a formula találni a származékos termék nem nehéz létrehozni egy táblázatot primitívek:
1.Pervoobraznaya nulla konstans.
2.Pervoobraznaya egység egyenlő X.
3.Pervoobraznaya az X X négyzete, osztva kettővel.
4. A primitív függvény X fokú en, en tartozik a természetes számok halmaza, X fokú en plusz egy osztva egy plusz en.
5.Pervoobraznaya egy funkcióval, osztva X a négyzet egyenlő mínusz egy, osztva a X.
6.Pervoobraznaya funkciót egy osztva négyzetgyök X egyenlő a négyzetgyöke két X, X jelentése nullánál nagyobb.
7. A primitív függvény x szinuszát mínusz a koszinusza X.
8. A primitív függvény X egyenlő a koszinusz szinusz X.
9. A primitív egy funkciót, osztva a szinusz-négyzet X egyenlő mínusz a kotangensét X.
10. A primitív egy funkciót, osztva a koszinusznégyzetes X egyenlő a tangensét X.

Tekintsük a példát találni primitív a különböző funkciókat.
Bizonyítsuk be, hogy a függvény egy primitív függvény. ha X egy primitív függvény a hatodik fokozat, a funkció megegyezik a hat-X az ötödik fokozat.
1. A definíció egy primitív, az y egyenlő nagy Aeff X nevezzük primitív függvény y egyenlő kis Aeff X előre meghatározott időközönként X nagy, ha bármely X tartozó ezt az űrt, a egyenlőséget.
2. Találunk nagy Aeff általános képletű származék a hálózati funkció. ez egyenlő a hat X az ötödik fokozat.
Kaptunk két kifejezést az egyenlőség, akkor definíció szerint egy primitív függvény ef nagy, X egyenlő a hatodik hatványával, egy primitív függvény ef kicsi, egyenlő hat X az ötödik fokozat.
A függvény (y egyenlő X ef kis) talál egy primitív, ha
(Ef az X egyenlő mínusz egy, osztva X a kocka).
1.Po meghatározása mértékben a negatív index képviseli a kifejezést mínusz egy, osztva a kocka X, formájában: X mínusz mínusz harmadik foka.
2. Miután megállapította képlet primitív hatványfüggvény, meg egy primitív függvény X eff egyenlő az X-mínusz mínusz harmadik erő.
Kapunk mínusz X, hogy a hatalom mínusz három plusz egy osztva mínusz három plusz egy.
Egyszerűsítése a kifejezés már mínusz X, hogy a hatalom mínusz két, osztva mínusz két, csökkentve a hátránya, megkapjuk az X, hogy a hatalom mínusz két osztani kettővel.
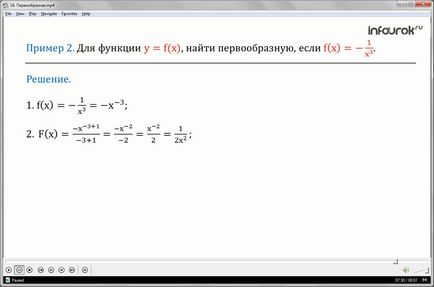
A definíció szerint a mértéke egy negatív index képviseli az expressziós formájában egy osztva két X négyzeten.
Így a primitív funkció x eff kis, egyenlő mínusz egy, osztva X a kocka, függvénye Aeff nagy, ami megegyezik a egy osztva két X négyzeten.