Építőipari vetítés síkidomok - plane - során ábrázoló geometria - rajzok, Theory,
Építőipari vetítési síkidomok (t. E. A számok, az összes pont, amely egy síkban fekszik, például egy négyzet, kör, ellipszis, stb. D.) csökken az építőiparban a nyúlványok pontok sorozatát, egyenes szakaszokból és görbe képező vonalak a kontúrok a nyúlványok számok. Ismerve a csúcsainak koordinátáit, például egy háromszög, lehet építeni a nyúlványok az ezeket a pontokat, majd az oldalán a nyúlvány, és így kapjuk vetítési formák.
A rajzok tartalmazzák a nyúlvány a háromszög találkoztak (például, ábra. 110, 112 és mtsai.). Ha összehasonlítjuk a szám. 110 és 112, látható, hogy ábrán. 110 az egyik kiálló, a front set, ábrázolja a „front” oldalán a háromszög és a vízszintes - „vissza”. A ábra. Nyúlványok mindegyike 112 mutat egy háromszög ugyanazon oldalán. Jelzés lehet kanyargós sorrendben csúcsok: Fig. 110 elülső vetülete az óramutató járásával megegyező irányban (jobbról A „C”) és a vízszintes - az óramutató járásával ellentétes; Ábra. 112 megkerülve mind a kiemelkedések csak egy irányba - a jelen esetben az óramutató járásával megegyező.
Általánosságban elmondható, hogy a rendszer π1. π2. π3 vetülete egy sokszög is poligonok az azonos számú oldala; ahol a sík a sokszög egy sík közös álláspont. De ha π1 rendszert. π2 mindkét előrejelzések, például, a háromszög egy háromszög, annak síkjában lehet egy sík vagy profilozott generikus kiálló: Fig. 112 - általános helyzetben sík, és ábra. 127 - profil-kiálló. Determináns, mint említettük p. 52 magyarázatában ábra. 127, vízszintes (vagy frontális) ha a nyúlvány π1 és π2 párhuzamosak egymással, a sík profil kinyúló (127. ábra); ha nem párhuzamos, a generikus síkban (például, ábra. 112, 115, bal).
Ha a vetülete a sokszög π1 vagy π2 egy vonalszakasz, a síkra, amely merőleges a sokszög, rendre π1 vagy N2. Például, ábrán. 123 a háromszög síkjában vízszintesen proetsiruyu- schaya, ábrán. 125 - első kiálló.
Ábra párhuzamosan elrendezett síkjával nyúlvány az előrejelzések szerint ez torzítás nélkül. Például, minden eleme a háromszög CDE, ábrán látható. 133 vetülő a téren. π2 torzítás nélkül; a kör ábrán látható. 140 előrejelzések a téren. π1 torzítás nélkül. -
Ha az az ábra síkjából nem síkjával párhuzamos vetítés, hogy meghatározzák a természetes formában (m. E. húzás nélkül) az ábra alkalmazni meghatározott módszerek továbbiakban az V. fejezet Persze, most már nem tudta, ezek a módszerek építésére, például, a természetes megjelenést a háromszög ábrán látható. 112, hosszát meghatározó mindegyik oldalán, mint a szegmens hossza (cm. § 13), majd létrehozható egy háromszög a talált szegmensek. Ugyanakkor megállapítást nyert, és a háromszög szögei. Cosi, például az építőiparban, a pásztázó
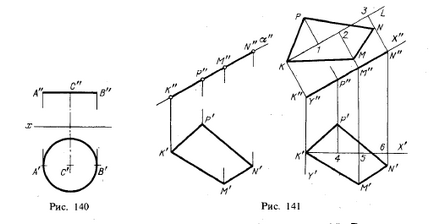
az oldalsó felülete egy piramis, prizma és munkatársai. (cm. További § 44). Ha a sokszög található kiálló a síkban, meg tudjuk építeni a természetes megjelenés ábrán látható. 141.
Tegyük fel, hogy határozzák meg a természetes megjelenést a négyszög KPNM, található az első kiálló téren. α. Ezután, ábrán látható. 141 a jobb, akkor megteszi a síkban az ábra két tengelye téglalap koordinátáit az elején legalább a K pont; 2. Az abszcisszán y tengely a merőleges π2 (a vetületét ezen a tengelyen K „Y”, K'Y „), felhívni egy egyenes vonalat KL (ez lehet tenni, például párhuzamosan az»X«) és tegye a K1 = K„R "K2 = K" M "SC = K" N. " Ezután, a merőlegesek a vonal KL pontokon 1,2 és 3 elhalasztja szegmensek P1 = R'4, M'5 és M2 = N3 = N'6. Épített így négyszög KMNP egy előre meghatározott, természetes megjelenést.
Megoldásában sok probléma, hogy az a kérdés, milyen pozícióban síkidom tekintetében a vetítési sík, alapvető fontosságúvá válik. Példaként azt a kérdést, építése négy Triangle Center.
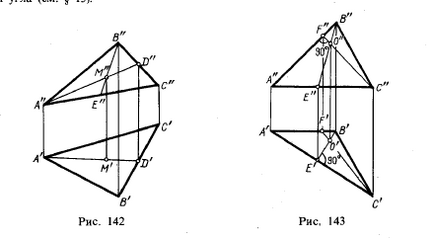
Mivel a szétválás vonalszakasz a térben megfelel fele azonos részlege a nyúlvány (lásd. § 12), az építőiparban a metszéspontja a a háromszög középvonalainak 1) állítható elő az ábrán, minden esetben közvetlenül. Elég (ábra. 142), a medián töltött az egyes a nyúlványok a háromszög, és a metszéspont annak mediánok fogja meghatározni. Így lehetséges, hogy korlátozza az építési, mind a nyúlványok egyetlen medián (például, A'D „és A»D«) és egy második medián nyúlvány (azaz például V»E«); metszéspontjában A „D” és B „E»megkapjuk az M pont«, valamint azt, hogy megtalálják A'D pont M '.
Az is lehet, megszerkesztésével csak egyik felező a háromszög, ezeken alapuló megtalálják az M pont ismert tulajdonságai a geometria a pont (mely elválasztja egymástól medián elleni 2 1).
Az építőiparban a metszéspont a három magasság egy háromszög 2) pontjában és merőleges a oldalán a háromszög átszívott közepén 3) kapcsolódó, a kölcsönösen merőlegesen vonalak.
1) A metszéspontja a a háromszög középvonalainak a súlypont.
2) a háromszög orthocenter.
3) A központ a körülírt kör.
A 15. § arra meghatározott feltételek, amelyek mellett a merőleges vonal szegmensek a térben vannak a nyúlványok is merőleges a szegmensek, ha a háromszög síkjával párhuzamos síkjában nyúlvány (például CDE háromszög ábrán. 133), majd, csepegés merőlegeseket a pontok C „D” és E „a másik oldalon is, megkapjuk a kiálló magassága a háromszög, de egy általános háromszög, így nem lehet csinálni,
Abban az esetben, ha az egyik oldalon a háromszög párhuzamos a téren. π1; és a többi párhuzamos MP, π2 (ábra, 143), amelynek C "F" merőleges az A "B" és a V'E 'merőleges A'C' get a térben, és CF⊥AV BE⊥AS; magasságok metszéspont épült nélkül speciális technikákat.
Ugyanebben az általános esetben kivitelezésére a vetítési rajz merőleges vonal van, hogy vegye igénybe speciális, a továbbiakban ismertetünk.
Felépítése a metszéspontja a szögfelezői a háromszög 1) is elő lehet állítani közvetlenül csak különleges esetekben, a háromszög viszonyított helyzete a vetítési síkok. Ez azért van, mert a kettéosztott egy vetítési szöget felező reagál a térben csak akkor, ha a szög a fél egyformán hajlanak arra a síkra vetítve, amely nyúlványok előállított kettéosztott szögben (lásd. 15. §).
Megszerkesztésében előrejelzések sokszög kell figyelni, hogy ne sérti feltétele a megállapítás minden pont a szám az azonos síkban
Ábra. 144 teljesen vízszintes vetülete ötszög ABCDE és az első vetülete csak három csúcsa: A „B” és E”, Jobb
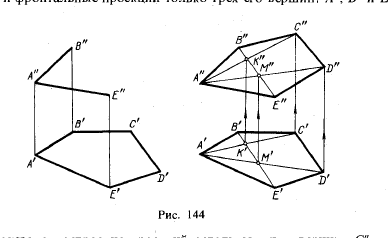
A 144. ábra a szerkezet a kiemelkedések a másik két csúcs, C „és D”, ötszög, hogy C és D pontok fekszenek által meghatározott síkban három pont A.
1) A központ a beírt kör.
B és E, szükséges, hogy azok a sorok síkjában fekvő ilyen vonalat AC átló, AD és BE vízszintes vetülete, amit lehet építeni. Az elülső vetülete ötszög levonhatjuk csak az „E”, de a gép a Pentagon metszéspontja az átlók a K és M, a vízszintes nyúlványok (K „és M”) áll rendelkezésre, és az első vetítés, megkapjuk egyszerre, ahogy kell alapulnia B "E". Két pont épített frontális kiemelkedés és a másik két átlója A „R” és A „M”, akkor kell lennie pont C „és D”, amely jellemzi a vízszintes előrejelzések.
Kör, amelynek síkja párhuzamos síkban a vetítési vetíti ez a sík torzítás nélkül (lásd, ábra, 140, ahol a kör középpontjától vízszintes síkban). Ha a sík a kör merőleges a vetítési sík, akkor ezt a síkot az előrejelzések, mint egy kör vonalszakasz egyenlő a a kör átmérője,
De ha a kör található a sík alkotó síkja vetülete egy éles szögben φ prognózis sávja egy alak úgynevezett ellipszis.
Ellipszis is nevezik görbe befoglaló ellipszis-alakú, ha ez a szám egy ellipszis-tartományban vetítés, az ellipszis-line egy vetülete kör. A következőkben, ha beszél az ellipszis, azt jelenti, a vetítés egy kör.
Ellipszis utal, hogy a száma görbék egy görbe másodrendű. Egyenletek a görbék derékszögű koordináta jelentenek másodfokú egyenlet. Másodrendű görbe metszi egyenes két ponton. Ezután újra találkozunk a parabola és hiperbola is a görbék a másodrendű.
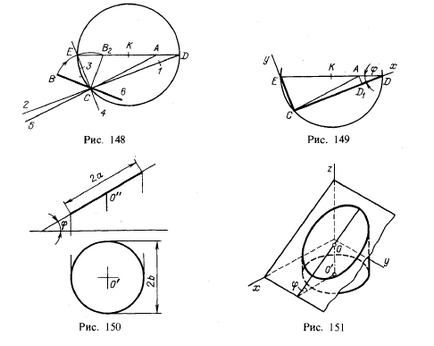
Ellipszis lehet tekinteni, mint „tömörítés” kör. Ez ábrán látható 145, hogy a bal, fel, hogy a sugárral OB OB1 késleltetett szegmens hossza b, ahol b 1), hogy az ellipszis a ponton K.
1) tól normalis (lat.) - egyenes.
Hogyan építsünk tengelye az ellipszis, ha tudja, konjugált átmérők?
Legyen C kapott konjugátum félig tengely A és CB (ábra. 148). A konstrukció a tengelyek az ellipszis:
- az egyik fél-tengelye konjugátum, például NE, csuklósan keresztül 90 ° -os szöget a másik felé (a helyzetben CB2);
- AB2 tölteni szegmens és ossza félbe;
- attól a ponttól, hogy a huzal sugarú körben COP;
- közvetlenül definiált szegmens AB2. továbbra is keresztezi a körben a D és E pontokat;
- végre közvetlen DC, hogy az irányt a nagytengely;
- végezzen az EU-ban - az irányt a kis tengely az ellipszis;
- Mi elhalasztja C1 = AE - fél nagytengely;
- Mi elhalasztja SOC = AD - kisebb tengelye;
- Mi elhalasztja C2 = C1 és C4 = NW, C5 = CA, CB = Sa.
Az ellipszis hajthatjuk keresztül nyolc pontot 1, A 3, B, 2, 5, 6, vagy 4, és épül a nagyobb és kisebb tengelyét ábrán látható. 147.
Tehát, kiadások közvetlen CD és CE, megvan az irányt a nagyobb és kisebb tengelyét az ellipszis; A pont tartozó ellipszis átmérőjű ED osztja két részre, melyek közül az egyik (AE) a fél nagytengely az ellipszis és a másik (AD) - kisebb tengelye. Ha (ábra. 149)
veszi a koordinátatengelyek x és y rendre a közvetlen CD és a CE és az A pont a elvégzésére AD egyenesre merőleges CD, a koordinátáit a pont lehet a következőképpen fejezhető ki:
Ez az egyenlet egy ellipszis, amelynek AE - fél nagytengely, egy AD - kistengelye.
Ábra. 146 ábra a szerkezet vízszintes vetülete kerületileg található a kiálló frontális síkban ferde a PL. π1. Tegyük fel most, hogy egy ilyen síkban egy ellipszis félig tengelyei a és b. A vetítés néha egy kör átmérője megegyezik a kisebb tengely az ellipszis: Ez az eset, amikor a síkja közötti szög, amely jogok az ellipszis és szögletes. π1 viszonyának cos? = B / a (ábra. 150).
A kapott kerülete a nyúlvány szolgál számos ellipszisek, ha a szög φ, hogy megváltoztassa a méretet, a, b. Változatlan marad Képzeljünk el egy jobbmenetes henger függőleges tengellyel (151. ábra); ferde szakasz a henger ellipszisek, a kisebb tengelye megegyezik a henger átmérője.
Kérdések §§20-21
- Mint látható a rajzon-frongalno kiálló síkot közvetlen általános helyzetét?
- Hogyan építsünk egy vetülete a súlypont egy adott háromszög rajzot?
- Mi lehet egy előrejelzési sáv, attól függően, hogy a helyzet a síkon síkjához képest vetítés?
- Meg tudjuk vizsgálni az ellipszis, mint a „tömörítés” kört?
- Mi a képarány az ellipszis?
- hogy az ellipszis van: a) a szimmetriatengely, b) a központ szimmetria?
- Mit átmérőjét ellipszis nevezik: a) a tengely, b) konjugált átmérők?
- Által meghatározott konjugátum átmérőjét az ellipszis építeni a tengelye?