Átlagos sebesség, az elmélet és az online kalkulátorok
Mozgatása anyagi pont
Hagyja, hogy a anyagi pont mozog az X-tengely minden alkalommal az egyik irányba. Ezután a mozgás az anyag szempontjából időintervallum $ \ Delta t = t_2-t_1 $ csökkenteni fogja a $ \ Delta x = x_2-x_1 $. Ha egy anyagi pont az idő az állásfoglalásra mozgatjuk az egyik irányba, a megtett távolságot ($ \ Delta s $) egyenlő az abszolút értéke elmozdulás:
\ [\ Delta s = \ left | \ Delta x \ right |. \ Left (1 \ right) \]
Ha a pont mozog először az egyik irányban, majd megáll mozog az ellenkező irányban (például, mint a test függőlegesen mozog vetett fel) az útvonal az összege elmozdulások a modulok mindkét irányban:
\ [\ Delta s = \ left | \ Delta x_1 \ right | + \ left | \ Delta x_2 \ right | + \ dots \ left (2 \ right) \.]
Meghatározása az átlagsebesség
Közepes sebesség ($ \ left \ Langle alagútrendszert v \ right \ rangle $) egy anyagi pont időintervallumban $ \ Delta t $ nevezett fizikai mennyiség, ami az aránya a mozgás, a test vállalta, hogy ebben az időszakban:
\ [\ Bal \ Langle alagútrendszert v \ right \ rangle = \ frac \ bal (3 \ jobbra). \]
átlagsebességet iránya ugyanaz, mint az utazás.
A egysége az a sebesség, az ilyen mozgást, amelyben az elmozdulás a ponton időegység alatt egyenlő egy hossza:
sebesség mértékegység (ideértve az átlagos sebesség), a Nemzetközi Mértékegység Rendszer (SI) a méter per másodperc:
Az átlagsebesség mellett változó vezetési
Ha nem egyenletes mozgást érték az átlagos sebesség erősen függ a választott időtartam a test mozgását.
Tekintsük a mozgás egy testület, amely szabadon esik lefelé. A törvény a mozgás egyidejűleg:
Az idő $ t_1 = 0,1 \ $ c test koordináta (helyettesítő időt $ t_1 $ általános képletben (4)) jelentése: $ x_1 = 0,049 \ $ m; A $ t_2 = 0,2 \ $ c $ \ x_2 = 0196 $ m $, míg \ left \ Langle alagútrendszert v \ right \ rangle $ időintervallumban a $ t_1 = 0,1 $ s $ t_2 = 0,2 \ $ c lesz:
Ha vesszük ugyanazt szabadon eső test közötti időtartam $ t_1 = 0,7 $ s $ t_2 = 0,8 \ $ c, az átlagos sebesség egyenlő lesz $ \ left \ Langle alagútrendszert v \ right \ rangle = 7,4 \ frac $.
Az átlagos sebessége egyenletes mozgás
Csak akkor, ha az átlagos sebessége egyenletes mozgás állandó és független az időintervallum, amelyben a test mozog. A egyenletes mozgás egy részecske az X tengelyen, hogy mozog a kinematikai egyenletek felírható:
Találunk az átlagsebesség a definíció (3) és a kifejezés (6):
Hogy értékelje a számszerű érték az átlagos sebesség a gyakorlatban használja a következő definíciót $ \ left \ Langle alagútrendszert v \ right \ rangle $: átlagos sebessége egyenlő arányban proydonnogo útvonal (ak) az idő (t), amely költöttek mozgás:
\ [\ Bal \ Langle alagútrendszert v \ right \ rangle = \ frac \ bal (7 \ jobbra). \]
Az így meghatározott átlagsebességet egy skalár mennyiség.
Példák problémák megoldás
Feladat. Gyalogos, töltött első felében az idő a mozgás, mozgás sebességgel 5 $ v_1 = \ frac $, a második fele az idő volt, amelynek mértéke a $ v_3 = 3 \ frac $. Mi az átlagos mozgási sebessége az ember?
Határozat. Készíts egy rajzot.
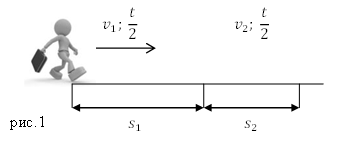
A probléma megoldása érdekében használjuk a formulát, amely meghatározza az átlagos sebesség:
\ [\ Bal \ Langle alagútrendszert v \ right \ rangle = \ frac \ \ bal (1,1 \ jobbra), \]
ahol az út két részből áll, a mozgás:
És a feltétele a probléma:
\ [S_1 = v_1t_1 = v_1 \ frac \ bal (1,3 \ jobbra) \ és \ \] \ [s_2 = v_2t_2 = v_2 \ frac \ bal (1,4 \ jobbra). \]
Helyettesítő definíciójában átlagsebesség (1.1) jobb oldalán a kifejezést (1.2) - (1.4), és vegye figyelembe, hogy a $ t = t_1 + t_2 $ van:
Kiszámítjuk átlagsebességgel gyalogos:
\ [\ Bal \ Langle alagútrendszert v \ right \ rangle = \ frac = 4 \ (\ frac). \]
Válasz. $ \ Left \ Langle alagútrendszert v \ right \ rangle = 4 \ frac $
Feladat. Mi az átlagos sebesség, ami volt egy anyagi pont időintervallumban $ \ tau $, ha az egyenlet a sebessége:
\ [V \ bal (t \ right) = A + Bt + Ct ^ 2 \ \ left (0 \ le t \ le \ tau \ right) \ left (2,1 \ jobbra). \]
Határozat. Ennek alapján a probléma megoldására a következő képlet segítségével ($ t = \ tau $):
\ [\ Bal \ Langle alagútrendszert v \ right \ rangle = \ frac \ \ bal (2,1 \ jobbra). \]
Mi megtaláljuk a módját egy anyagi pont, mivel a sebességi egyenlet az alábbi feladatokat:
Helyettesítse a jobb oldali (2.2) a (2.1), van: