A logaritmikus spirál, történelmi adatok meghatározását, a logaritmikus spirál, épület
történelmi adatok
Meghatározása logaritmikus spirál
A logaritmikus spirál - egy görbét, amely metszi a sugarak egy pontjából kilépő O azonos szögben.
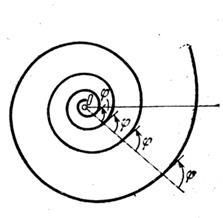
Az egyenlet a görbe poláris koordinátarendszerben
A távolság a tekercsek együtt növekszik szöget.
Építése a logaritmikus spirál
hiperbolikus spirál Archimedes logaritmikus
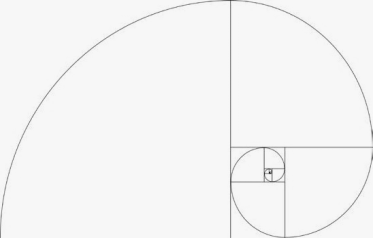
Logaritmikus spirál alkalmazásával hozhatunk létre az úgynevezett „arany téglalap”, azaz e, amelyben az oldalarány egyenlő az arany arány:
Ha az arany téglalap vágott négyzet egy oldala megegyezik a kisebb oldalon a téglalap, akkor megint kapunk egy aranyszínű téglalap, de kisebb. Ha továbbra is ez a folyamat leírását, majd csatlakoztassa egy sima görbe csúcsai a négyzetek, akkor megkapjuk a logaritmikus spirál. Pont elosztjuk oldalán a téglalap közepén és extrém tekintetben hazugság logaritmikus spirál, csavar benne.
I. Nézzük meg a hossza az ív egy logaritmikus spirál
0 # 63; # 63; 2, a következő képlet segítségével:
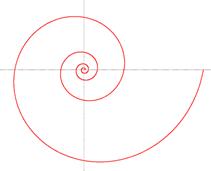
II. Kiszámoljuk a terület az ábra által határolt első logaritmikus spirális tekercset a következő képlet segítségével:
A főbb jellemzői a logaritmikus spirál
1. A bezárt szög az érintő egy tetszőleges helyen egy logaritmikus spirál sugara vektor az érintési pont, állandó és függ csak a beállítást.
2. A paraméter m határozza meg, hogy milyen szorosan van, és milyen irányban van csavart spirál. Határesetben, amikor = 0 a degenerálódó spirál sugara kör. Fordítva, ha hajlamos a végtelenig (hélix közelít egy egyenes vonal. Az a szög kiegészítő 90 °, Tilt úgynevezett spirális.
3. A méret a logaritmikus spirál tekercs fokozatosan nőtt, de alakjuk változatlan marad.
4. Ha a szög növekszik vagy csökken számtanilag, akkor növeli (csökkenti) egy geometriai.
5. Fordítsa a sarki tengely körül a pole, lehetséges, hogy elérjék a teljes megsemmisítése a paraméter, és csökkenti az egyenlet a forma r =, ahol - egy új paramétert.
6. A görbületi sugár minden ponton arányos a spirális ív hossza a spirál a kezdetétől eddig a pontig.
A logaritmikus spirál jellegű
A logaritmikus spirál - az egyetlen típusú spirál, amely nem változtatja meg az alakját a növekvő mérettel. Ez a tulajdonság megmagyarázza, hogy miért logaritmikus spirál, így gyakran előfordul a természetben.
Animal Kingdom biztosít számunkra példát spirálok kagylók, csigák és kagylók.
Mindezen formák arra utalnak, természeti jelenség: a kanyargós folyamat kapcsolódik a növekedési folyamatot. Tény, hogy a csigaház - ez nem más, se kevesebb, mint a kúp, feltekerve is. Ha jobban megnézzük a növekedés a héj és a szarvak, tudomásul vesszük, egy másik érdekes tulajdonsága: a növekedés akkor csak az egyik végén. És ez a tulajdonság megtartja alakját teljesen egyedülálló a görbék matematikai, logaritmikus vagy egyenlő szögű spirál.
Galaxy, a viharok és hurrikánok nyújt lenyűgöző példája logaritmikus spirál.
Végül, minden olyan hely, ahol van egy természetes jelenség, amely egyesíti a tágulás vagy összehúzódás a forgatás egy logaritmikus spirál.
A növényi világ példák feltűnő, mert a növény lehet végtelen számú spirálok és nem csak az egyik tekercs mindegyik.
Elhelyezkedés vetőmag bármely napraforgó, mérlegek akár egy ananászt és számos más típusú növényekre, egyszerű margaréta ... ad nekünk egy igazi parádéja összefonódott hélix.
A pók szövi a hálóját spirálisan.
A logaritmikus spirál a szakterületen
Alkalmazása a logaritmikus spirál a szakterületen alapján a tulajdonsággal, hogy minden kereszt ívsugár vektorok ugyanolyan szögben.
Így forgó lapátok különböző vágógép profiloldalaim alakos spirál ív, ezáltal vágási szög (a szög a penge és az irányt a forgási sebesség) állandó marad mentén mozgó kés éle, amely kisebb kopás.