5. lehetőség
Feladat 14. Dana szabályos hatszög hasáb, a hossza minden él egyenlő 1.
a) Construct részén áthaladó két átellenes széle a prizma bázis.
b) Find a keresztmetszeti területe.
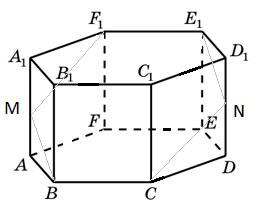
a) Két szemközti szélei egy szabályos hatszög hasáb, ez pl, BC és a bordák. Szakasz a bordán keresztül lesz egy hatszög, áthaladva a M és N pontok feküdt a felezőpontja a szegmensek és rendre (lásd. Ábra).
b) Tegyük fel, hogy az a szög között az alap részt, és a prizma egyenlő. Akkor tudjuk írni a következő egyenlet
ahol - a bázis a prizma; - a terület a kívánt részt. Ebből a képletből fejezzük keresztmetszeti területe, kapjuk:
Engedje meg, hogy egy derékszögű háromszög BFF1 mint az arány a szomszédos láb átfogója BF BF1. BF találja az irányt a háromszög ABF. Ebben a háromszög az a szög 120 fok. AB és az AF egyenlő 1. Azután a tétel a koszinuszok, van:
Most tekintsük a derékszögű háromszög, és kiszámítja az irányt a Pitagorasz-tétel:
Így a koszinusza a szög a síkok közötti egyenlő
Most kiszámítani a tér hasáb alapja. Mivel a bázis egy szabályos hatszög, ez lehet osztani hat egyenlő oldalú háromszög, amelynek az oldalai egyenlő 1 (mivel minden az arcok a bázis egyenlő 1). Mint ismeretes, a terület egy egyenlő oldalú háromszög, és a = 1. Ezután a területet a hatszög egyenlő
Végül, a keresztmetszeti területe egyenlő a