Példák járó problémák megoldása elektromosság és mágnesesség
Megoldás: A térerősség A pontban (. 3. ábra) által a szuperpozíció elve alapján is:
A tétel az koszinuszok:
Kaland ponttöltés területeken:
By hipotézis tehát. majd:
és az eredő erő egyenlő:
Jelöljük AB = h. majd
A tétel Pitagorasz:
Lehetséges φ kapott mezőt pont van:
A potenciális által gerjesztett ponttöltés egyenlő:
De az állapotot. Majd így:
A: E = 480 V / m; φ = -40 V.
Probléma 2. Egy elektron gyorsítható egy potenciális különbség 6 kV-os, legyek egy homogén mágneses mezőt szögben 30 °, hogy a villamos tér irányában, és kezd forog. Indukciója a mágneses mező B =. Keresse meg a sugár a menetek és a pályán a spirál.
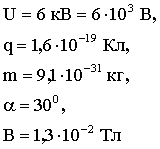
Megoldás: A sebesség az elektron lesz megtalálható a feltétellel, hogy a működése az elektromos erőtér költik a változás kinetikus energia az elektron:
A = Aw. A munka az elektromos mező megegyezik a termék a töltést a potenciális különbség: A = qU. A kezdeti kinetikus energia egyenlő nulla, így a Aw = W. Ezért:
Bővítjük az elektron sebessége, belép a mágneses mező két összetevőből áll: - sebesség komponenssel mentén irányul erővonalak u sebesség komponenssel merőleges a erővonalak. Ábra. 4:
A vetítés a elektron pályája a merőleges síkban, egy kör, ezért a Lorentz-erő említett szokásos részecske (centripetális) gyorsulás. Lorentz erő:
ahol R - a kör sugara. Szerint a Newton második törvénye: F = ma.
kezelés időtartama:
Mivel a részecske sebességének van egy összetevője, a részecske pályája egy spirál. helix pályán:
Ellenőrzése méretek számítási képletek (2) és (3).
A méret a termék [q] · [B] találunk a kifejezés a Lorentz-erő:
Szerint a Newton második törvénye: F = ma, azaz
Behelyettesítve számszerű értékek (1), (2) és (3).
Válasz: R = 1 cm, h = 11 cm.
Probléma 3. Banki Ring 10 cm sugarú fekszik az asztalon. Mi a vád áramlását a gyűrű, ha a turn egyik oldalról a másikra. Ellenállás Ring 1 ohm. A függőleges összetevője a Föld mágneses mező indukció 50 mT.
Megoldás: A definíció szerint a jelenlegi egyenlő a származék, a töltési idő:
Ezért a vád, hogy átfolyik egy karmester, határozza meg:
Szerint Ohm-törvény zártláncú áram erőssége egyenlő:
ahol ε - EMF forrás, R - az áramkör ellenállása.
A jelenlegi a gyűrű jelenik miatt EMF indukció. Ezért. EMF indukciós találunk a törvény Faraday-Lenz:
ahol - az arány a mágneses fluxus változási.
Behelyettesítve (3) be (2):
Behelyettesítve (4) be (1):
Integrálása (5), kapjuk:
ahol - a mágneses fluxus áthatoló a gyűrű után forgó ugol180?;
- mágneses fluxus forgatni. és kiszámítjuk a következő képlet:
ahol B - a mágneses indukció, - a terület a gyűrű, α - közötti szög merőleges a gyűrű terület és vonalak az indukció.
A méret az induktor megtalálható a törvény
Kiszámítjuk q. Vegye figyelembe, hogy a fordulási területen normális a gyűrű párhuzamos vektor. Ezért α1 = 0. A reakcióelegyet szokásos forgási ellentétes irányú vektor. Ezért, α2 = 180 °. majd: