Geometriai ábrázolása komplex számok 1

Vannak az alábbi formák a komplex számok: algebrai (x + iy), a trigonometrikus (R (cos

+ISIN)), Az exponenciális (újra i ).

Bármilyen komplex szám z = x + iy képviselheti az xy síkban, mint egy pont (x, y).

A sík, amelyen képviseli komplex számok, az úgynevezett a sík a komplex változó z (szimbólum készlet egy síkban z).

A tengely OX - valós tengelye, azaz rajta valós számok. DU - a képzetes tengelyének képzetes számok.

x + iy - algebrai formájában a komplex szám.

Levezetjük trigonometrikus forma egy komplex szám.

;

Behelyettesítve a kapott értékeket a kezdeti forma: azaz

R (cos

+ISIN) - trigonometrikus forma egy komplex szám.

Az exponenciális forma a komplex szám következik Euler-képlet, majd

Z = rei

- exponenciális formáját a komplex szám.

Cselekvési komplex számok.

3. szorzás. z1 z2 = (x1 + iy1) * (x2 + iy2) = x1x2 + i (x1y2 + x2y1 + iy1y2) = (x1x2-y1y2) + i (x1y2 + x2y1);

4. osztály. z1 / z2 = (x1 + iy1) / (x2 + iy2) = [(x1 + iy1) * (x2-iy2)] / [(x2 + iy2) * (x2-iy2)] =

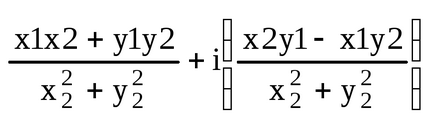
Két komplex számok, amelyek csak a jele az imaginárius egység, azaz a z = x + IY (Z = X-iy), az úgynevezett konjugált.

- Ha a komplex számok meghatározása a trigonometrikus formában.

Ezután a terméket z1 * z2 komplex számok: azaz termék modulus a termék a modulok és az érvelés érv az összege tényezők.

- Ha a komplex számok vannak megadva exponenciális formában.

; ;

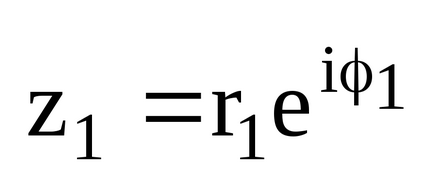
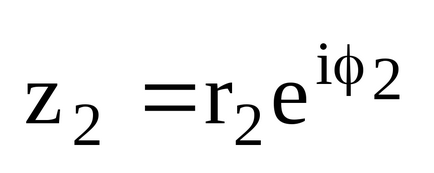
- Ha a komplex számok meghatározása a trigonometrikus formában.

- Ha a komplex számok vannak megadva exponenciális formában.

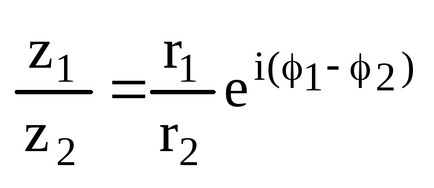
Hatványozás.

1. Egy komplex szám van beállítva algebrai formában.

z = x + iy, Z n, akkor megtalálja a newtoni binomiális képlet:

- kombinációk száma n elemeinek m (a számos módon, mint lehetséges, hogy az elemek a n m).

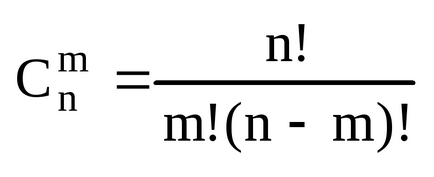
Kizárólag a komplex szám.

Ebben a kifejezésben kell helyettesíteni az értékek fok i:

0 i = 1 Ennélfogva, az általános esetben megkapjuk: i = 4k 1

i 31 = I 28 I 3 = -i

1063 i = i i = i 1062

2. Ha egy komplex szám megadott trigonometrikus formában.

Ahol n lehet „+” vagy „-” (egész szám).

3. Ha egy komplex szám megadott exponenciális formában:

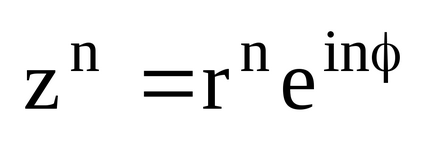
A megoldás az, gyökér n-edik hatványa a komplex szám z:

.

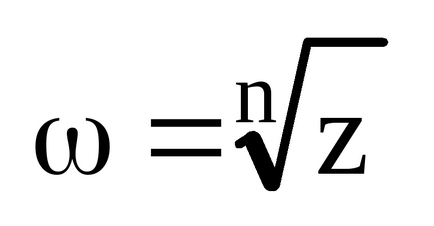
A gyökér n-edik hatványa a komplex szám Z pontosan n oldatokat (értékek). A gyökér a jelenlegi n-ed-fokú csak az egyik megoldás. A komplex - n megoldásokat.

Ha a komplex szám van megadva a trigonometrikus alakban:

Z = R (cos

+ISIN), A gyökér n-edik hatványa z képlet adja meg:

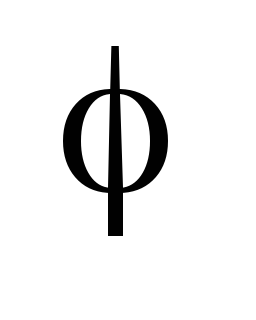
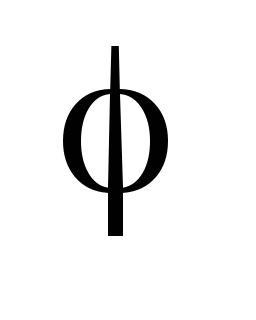
Soraiban. Numerikus sorozat.

Hagyja, hogy a változó és azon egymás értékeit a1, a2, a3, ..., AN. Számozása számsor hívják szekvencia. Ez a végtelen.

Numerikus sorozat egy expressziós A1 + A2 + A3 + ... + An + ... =

. A számok az a1, a2, a3, ..., AN - tagjainak száma.

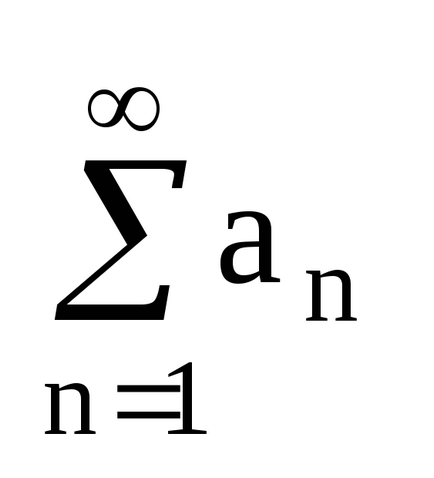
A1 - az első tagja a sorozat.

AN - n-edik vagy általános kifejezés a sorozat.

Számos tekinthető adja, ha ismert, n-edik (az általános kifejezés a sorozat).

Számegyenes végtelen számú kifejezést.

Számlálók - számtani sorozat (1,3,5,7 ...).

Nevező - exponenciálisan. bn = b1 q n-1;

.

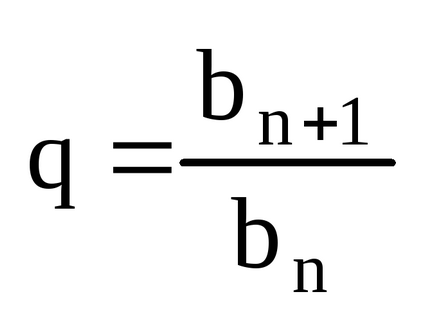
Tekintsük az összeg az első n a sorozat, és hagyta, hogy Sn.

Sn - n-edik részösszegként a sorozat.

Sorozat konvergál. Ha ezt a határértéket véges (véges határérték létezik S).

Számos eltérő. Ha ez a határ a végtelen.

A jövőben célunk: hogy állítson be egy számot.

Az egyik legegyszerűbb, de gyakran találkozott a sorozat egy mértani.

Mértani yavlyaetsyaskhodyaschimsyaryadom. ha

, és az eltérő, ha.

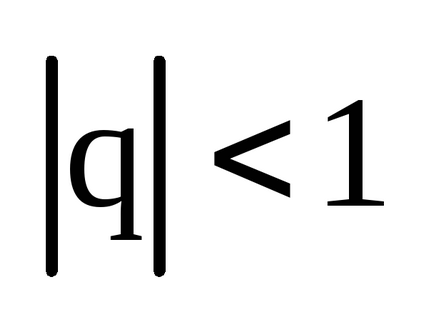
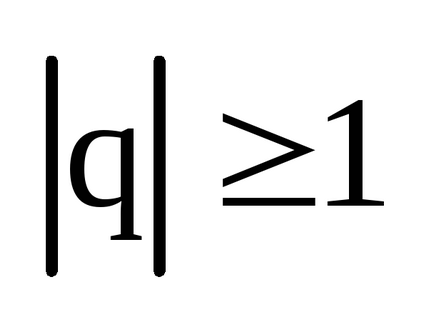
harmonikus sor (a sorozat) is megtalálható. Ez ryadraskhodyaschiysya.

Kapcsolódó cikkek

• Geometriai ábrázolása komplex számok