A minimális diszjunktív normál forma
Minimalizálása funkciókat. Karnaugh térképet. A digitális technológia // EG Lab [14:20]
A minimális diszjunktív normál forma (MDNF) logikai függvény - ez elrugaszkodott a minimális számú elemi kötőszavak a minimális számú érv (akár saját maguk vagy tagadás) ezt a funkciót. Ebben az esetben az igazság táblázat logikai függvény és annak MDNF mérkőzés.
A minimális diszjunktív normál forma a logikai funkció számos érv négy lehet előállítani Karnaugh térképeket. Ehhez Karnaugh térképezési egységek egymás alá tartozó téglalapok 4 × 2, 4 × 2, 2 × 2, 4 × 1, 1 × 4, 2 × 1, 1 × 2 és 1 × 1. Ezután elemi conjuncts MDNF épült.
n - a számos érv a függvény;
k - számos téglalapok a térképen Carnot;
argJ (i, l) - xj argumentum érték a sor érvek a cella (i, l);
[Math] F_ (x_1, x_2, \ ldots, x_n) = \ bigcup \ limits_ ^ k \ bigcap \ limits_ \ arg_j \ left [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = 1 \ Szöveg \\\ arg_j \ left [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = 0 \ End> y_j [/ math], ahol [math] y_j = \ beginx_j \ text \ \ arg_j \ left [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = 1 \\ \ bar_j \ szöveg \ \ arg_j \ left [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = 0 \ end [/ matematikai] [matematikai] \ arg_j \ left [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = \ begin1, \ szöveg \ \ forall (i, l) \ in P_t (x_1, x_2, \ ldots, x_n), \ arg_j (i, l) = 1 0 \\, \ szöveg \ \ forall (i, l) \ in P_t (x_1, x_2, \ ldots, x_n), \ arg_j (i, l) = 0 \ end [/ matematikai]
Példák építési MDNF
Építsük Karnaugh térkép funkciója három változó:
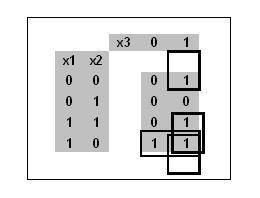
Units Karnaugh térképen minimálisan által lefedett egy téglalap formában 1 × 2 és a forma két téglalap 2 × 1, amely megfelel a három általános összefüggésben két érv. Megjegyezzük, hogy a két részleges téglalap típusú 2 × 1 téglalap megfelelnek az egy teljes bevonatot.
Építsük Karnaugh térkép funkciója négy változó:
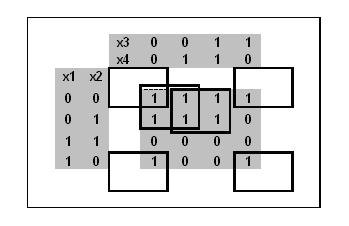
Units Karnaugh térképen minimálisan által lefedett három négyzet formájában 2 × 2, amely megfelel a három általános összefüggésben két érv. Megjegyzendő, hogy a négy sarkában egy négyzet hiányos megfelelnek egy teljes bevonat négyzet.
Építünk egy háromdimenziós Karnaugh térkép funkciója öt változó:
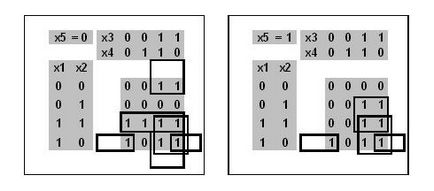
Egységek háromdimenziós Karnaugh térképen minimálisan lefedett parallelepipedonok alkotnak 2 × 2 × 2, 2 × 2 × 1 (kettő), 1 × 4 × 1 × 2 × 1 2, amely megfelel egy elemi összefüggésben két érveket, és négy elemi összefüggésben három érv. Megjegyezzük, hogy a szélsőséges, mindkét oldalán szögletes formák kombináljuk.