1. Alapfogalmak és meghatározások számítógépes aritmetika
Számítógépes aritmetika - olyan elveket és formák bemutatása számszerű adatok, eljárások és algoritmusok aritmetikai és számítása elemi függvények tekinthető szinten belső szervezeti felépítését, a technikai eszközök a számítógépes rendszerek (CS). Ez része a számítógépes matematika-orientált logikai szintű leírást számítási struktúrák és folyamatok bennük.
Mi az információs általában az általános értelemben vett? Az információ kifejezés származik a latin szó információt, ami azt jelenti:
Algoritmus - eljárás átalakítására információkat, amelyek által meghatározott véges szabályrendszer. Az információ képviselteti magát, mint számsor (egész szám) egy bizonyos jelölést, maguk a számok jelek megjelenítésére, amelynek véges kvantálási szintek száma.
számozási rendszer (SS) - a szabályok és technikák megállapítása egyértelmű közötti levelezés bármilyen számot és a képviselet formájában több karakter (szimbólumok).
Mennyiségi azonos számban (KECH) - egy szám, amely egyedileg számának megfelelő. (Függetlenül attól, hogy a számozási rendszer és mérési intuitív szinten abstract). Minden jegyű számot a rekord képest számos kifejezett ez a szám, és az úgynevezett mennyiségi azonos számban (KEC).
Hosszúság - a pozíciók száma (bitek) a bejegyzés számát. A technikai szempontból hossza úgy értelmezni, mint egy bit hosszúságú a rács (RSM). Különböző SS jellemezve változtatásával a vitarendezési egyetértés köteles rögzíteni ugyanazt a számot.
Minden művelet végre COP sorozataként térben és időben, néhány a legegyszerűbb, alapvető műveletek úgynevezett mikro-műveleteket. A fő osztálya mikro-ops a következők:
1) átvitel (vétel, kiadása) operandusok;
2) eltolódás (számtani, gyűrűs, logikai, módosított) az operandus által egy előre meghatározott számú bitből áll;
3) hozzáadásával vagy kivonásával a operandus egység azt (az általánosabb esetben - állandó érték);
4) összehasonlítás operandusok (az az elv, a „több - kevesebb - van”);
5) a bitenkénti logikai műveletre (diszjunkcióját összefüggésben, egyenértékűség, modulo-2);
6) számtani hozzáadásával a két operandus megfelelő számokat az azonos radix;
7) transzformációs operandus kódok (beleértve inverzió, kívül, titkosítás, dekódolás, stb).
2 Számrendszerek
Amint azt a fejezet száma rendszer - a szabályok és technikák megállapítása egyértelmű közötti levelezés bármilyen számot és a képviselet formájában több karakter (szimbólumok). Rekord számos rendszer az úgynevezett kódszámot. Röviden szám van írva a következő:
ahol: A - a mennyiségi ekvivalens (A);
(An-1 ... .a2 a1 A0) - a több számjegyet, amellyel, hogy képviselje a számát (A).
Egy külön pozícióját a kép számát nevezzük pozíciójáról szám - jegyű szám. A bitek száma egy rekord hívják jegyű szám, és egyenlő a hossza. A műszaki szempontból hossza úgy értelmezni, hogy egy kicsit hosszú a rács. Ha az ábécé (p) különböző értékeket, a bit (ai) tekinthető, mint az egyik (p-ed rendű) ábrán, amely lehet rendelni az egyes (p) értékek. Minden számjegy (aі) az (A) megfelel egyedileg annak mennyiségi (numerikus) egyenértékű - (K (aі)). A mennyiségi ekvivalens - (Kech) - (A), egy bizonyos előre meghatározott számú rendszer, a függvénye ekvivalens száma minden számjegy, azaz.:
ahol: R (A) - kvantitatív ekvivalens (A);
K (AN) - a maximális mennyiség (szám) egyenértékű a számjegyek száma (A) található a bal oldali számjegyet;
K (A0) - minimális mennyiség (szám) egyenértékű a számjegyek száma (A) található a jobb szélső kisülési;
Ezután bármely véges bites rács KECH (A) kerül sor mennyiségétől függően ekvivalens értékeket az egyes bitek K (A) min K (A) max. képviselet tartomány (D), a számok számos rendszer - a valós tengelyen intervallum tartalmazza a maximális és minimális szám képviseli egy előre meghatározott hosszúságú szót (bit hosszúságú mesh):
ahol: D - a tartományban ábrázolható számok egy bizonyos jelölést;
R (A) (p) max - maximális mennyiségi ekvivalens (A) a bázis (p);
R (A) (p) mіn - minimális mennyiségi ekvivalens (A) a bázis (p).
Bármennyi rendszer célja a gyakorlati használatra, biztosítania kell: - a képesség, hogy képviselje bármilyen számot egy adott tartományon belüli számokat; - egyediségét bemutatása; - légszomj és az egyszerűség a számok; - könnyű mastering a rendszer, valamint a könnyű és kényelmes működtetés.
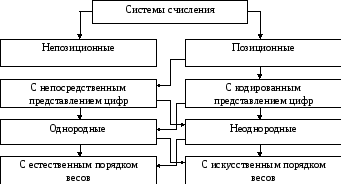
Besorolás 2.1 számú rendszerek
Jelenleg megkülönböztetni pozicionális számrendszer és nonpositional. Osztályozása számrendszert ábrán látható. 2.1.