5. téma egyenletek degenerált mag - studopediya
Van egy fontos osztályát integrálegyenletek hogy meg lehet oldani könnyen csökkentve azt az algebrai egyenletek. Ezek szerves egyenletek úgynevezett degenerált mag.
Definíció: A kernel az integrál egyenlet az úgynevezett degenerált, ha felírható az összeg a véges számú tagra, amelyek mindegyike egy termék két funkció, az első csak attól függ, x, és a második - csak # 958;:
Úgy gondoljuk, hogy folytonos [a, b], és hogy csakúgy, mint lineárisan függetlenek.
(1) egyenlet a formája:
Behelyettesítve (29) be (1):
Ettől. lineárisan független,
Megoldása a rendszer (32), ily módon fogjuk megoldani ezt a szerves egyenletet és az alábbi képlet segítségével (29). Ha az algebrai rendszer (32) nem megoldható, akkor így a integrál egyenlet.
D (# 955) - a polinom foka ≤ n, ahol a D (# 955;) ≠ 0, mivel # 955 = 0, D (0) = 1. Ezért, D (# 955;) van ≤ n különböző gyökerek.
D (# 955;) az úgynevezett meghatározó Fredholm az (1) egyenlet.
1. Ha # 955; oly módon, hogy D (# 955;) ≠ 0, akkor (32), és így a (1) egyenlet egyedülállóan képlet által meghatározott (29). Ebben az esetben, az f (x) = 0, és így a rendszer (32) van egy egyedi megoldást; ezért # 966; (x) = 0. Ez azt jelenti, hogy ezek a # 955;, ahol D (# 955;) ≠ 0, nem a sajátértékek.
Következtetés. ha # 955; nem egy megfelelő értéket, akkor az egyenlet (1) van egy egyedi megoldást.
Nyilvánvaló, hogy az inhomogén egyenlet (1) van egy egyedi megoldás bármilyen f (x) (
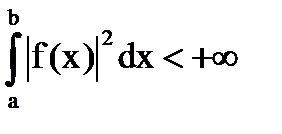
Megjegyzés: Az általános szabály, a megoldás a szerves egyenletek gyakran kénytelenek a közelítő módszerekkel. Fontos megállapítani megoldhatóságának egy tetszőleges jobb oldalán (az első tétel). Az előnyös az, hogy bizonyítani, hogy a homogén egyenletet, vagy átültetett rá (konjugátum) csak a triviális megoldás. Ezért, 1. tétel magában megoldhatóságának az inhomogén egyenlet.
Három alaptétele Fredholm vonatkozó oldhatósága egyenletek degenerált magok, és meg lehet hosszabbítani egy tetszőleges folytonos mag.
Keresse az egyenletek megoldása szinguláris kernelek:
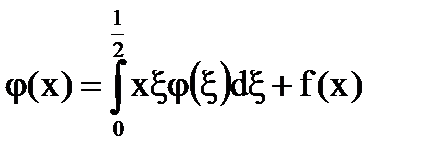
Megoldás: Legyen
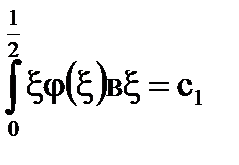
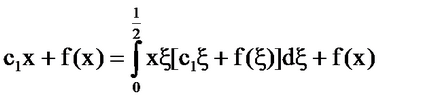
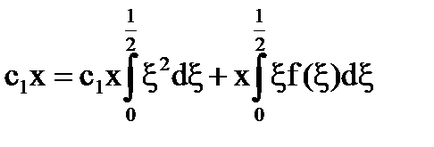
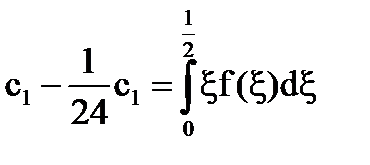
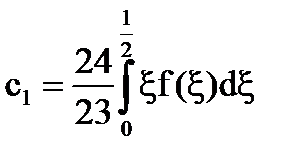
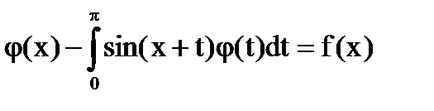
[5] által a formája:
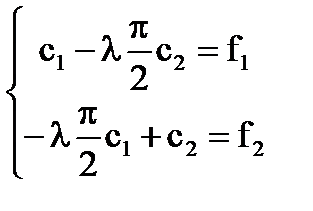
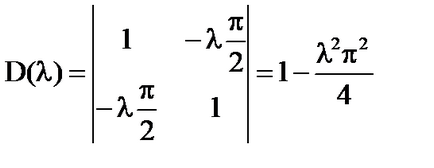
D (# 955) = 0; ; - sajátértékei az egyenlet.
ha # 955; ≠. # 955; ≠. A D (# 955;) ≠ 0, és a rendszer egy egyedi megoldást:
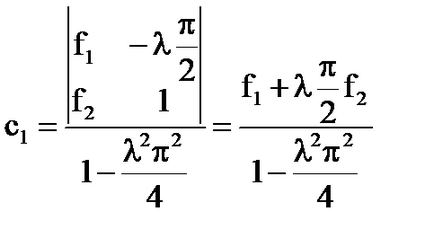
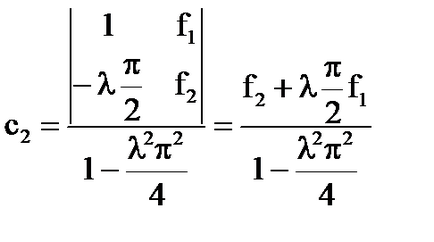
- Az egyetlen megoldás az integrál egyenlet
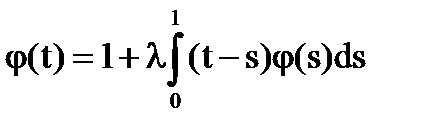
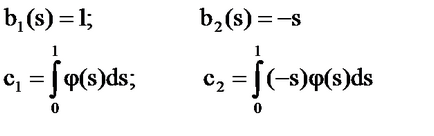
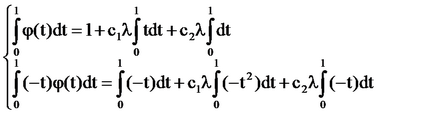
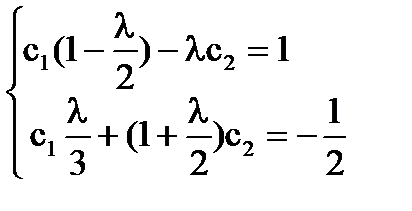
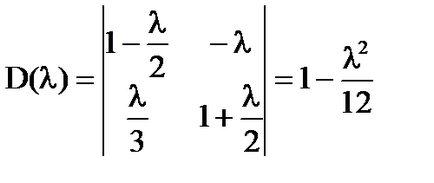
D (# 955;) ≠ 0 bármely valós # 955;.
A Cramer szabály
Ha. Az egyetlen megoldás az egyenlet
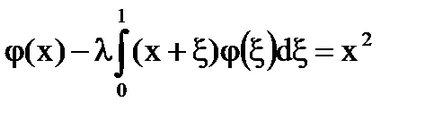
Megoldás: = x + # 958; - folyamatosan a négyzet 0 ≤ x, # 958; ≤1 és degenerált.
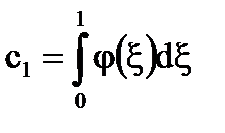
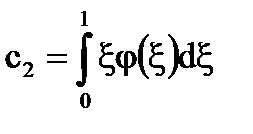
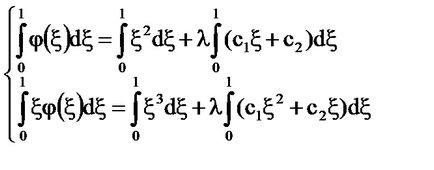
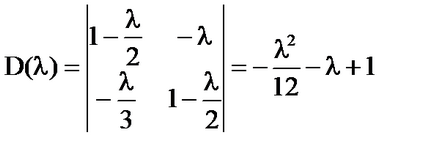
Ha. az egyetlen megoldás
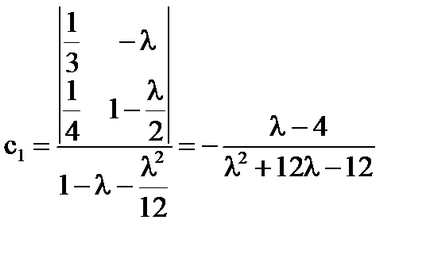
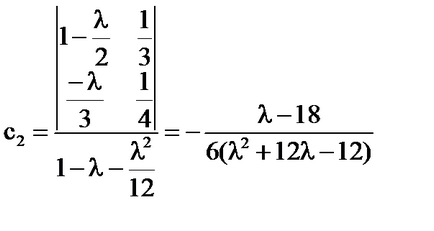
-
egyedi megoldás.
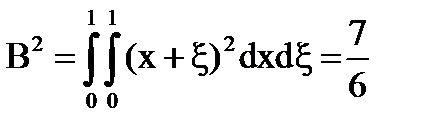
A megoldás létezik, egyedi, és megtalálható a módszer az egymást követő közelítések a
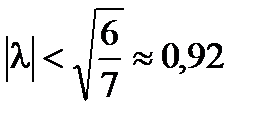
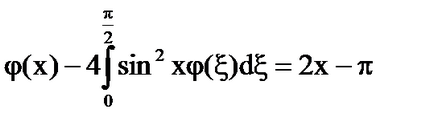
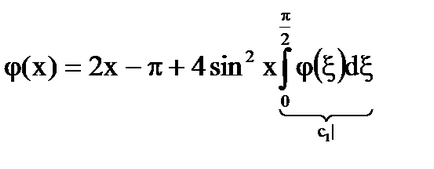
Megoldás: Core - degenerált.
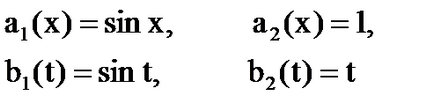
A képletek [6] - [7], számolunk
[5] által válik
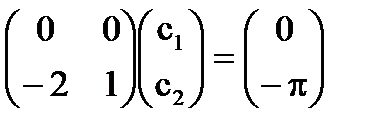
= C, = -π + 2C, ahol C - tetszőleges konstans.
Válasz: Minden függvénnyel
a megoldást az integrál egyenlet és egyéb megoldásokat az egyenlet nem.
gyakorlatok:
Problémák szerves egyenletek degenerált mag